2 干涉消除方式

    1. 旋转刀轴方式

    在一个刀位点处，曲面特征点于刀具系发生干涉的有m个，综合考虑m个干涉点的干涉情况，可找到一个消除干涉的最佳方向，以便最有效地消除刀具干涉。为此，引入了"干涉消除平面"的新概念，把m个干涉点处的曲面法矢量投影到刀具坐标系T的XTYT平面上，设干涉点处的曲面法矢量在XTYT平面上的投影为nxyi(i=1，2，…，m)，干涉点在XTYT平面上的干涉分量为 t(i=1，2，…，m)。如图4所示，则干涉消除矢量I可由下式求出

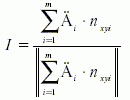    (4)

    由式(4)求出干涉消除矢量I(Sx，Sy，Sz)之后，再由干涉消除矢量I 和ZT轴构成干涉消除平面。设由轴ZT和消除矢量I的叉乘矢量为K，在平行于"干涉消除平面"的平面上计算刀具绕K 轴向I倾斜多大的干涉消除角度 能刚好消除刀具干涉，如图5所示。设将干涉点Pi(i=1，2，…，m)排除在刀具系表面之外所需要的最小角度为 i(i=1，2，…，m)，则干涉消除角度 是所有角度 i的最大值

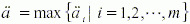    (5)

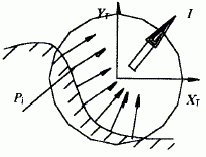
图4 干涉消除矢量I

图5 环形刀加工时消除角度(干涉消除平面2D 图)

    要把干涉点Pi排除在刀具系之外，干涉点Pi固定不动，刀具系绕K 轴向I方向旋转，等价于干涉点Pi相对于刀具系和刀具坐标系在平行干涉消除平面IOTZT的平面内转动 i角度，下面以环形刀为例加以分析。

    如图5 所示，环形刀加工时刀具系的旋转轴经过消除平面IOTZT与刀具圆环面的交圆弧中心点O1，并平行于矢量K，过干涉点Pi，平行于消除平面IOTZT作一截平面，截平面与刀具圆环面的交线为4次曲线，与圆柱面的交线为两直线。环形刀的刀轴旋转分两种情况，当干涉点Pi落入环形刀圆柱体内，旋转角度 i为∠PiOPi‘(图5a)，计算公式为

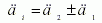    (6)

    而角度1计算如下

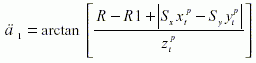    (7)

    当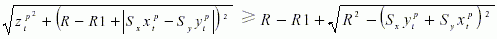时，点Pi在旋转过程中与圆柱表面截线相交， 2的计算公式为

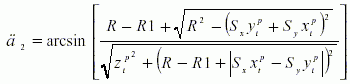    (8)

    当点Pi在旋转过程中不与圆柱截线相交时，则点Pi‘可能与圆环截面4次曲线或刀具底平面截线相交。与圆环截面4次曲线相交时，角度 2的计算较复杂，为了简化计算，对旋转角度作保守处理。这时，计算出的角度 2要比实际角度大，但对于刀具干涉处理没有影响。保守处理点Pi‘均旋转到与刀具底平面相交，这时角度 2等于

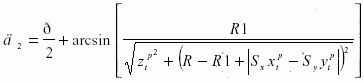    (9)

    如图5(b)所示，当干涉点Pi落入环形刀圆环体内，同样对旋转角度作保守处理，点Pi‘均旋转到与刀具底平面相交，旋转角度 i为∠PiOPi‘，计算公式同式(6)，其中角度 1和 2的计算如下

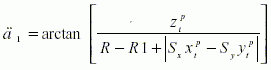    (10)

    (11)

    当式(11)中的分母小于分子时，点Pi‘在旋转过程中不能与刀具底平面相交，这时不能通过旋转刀轴方式来消除干涉，但这种情况可能性极小。

    同理可处理动力头圆柱体内的干涉点。

    虽然刀具系可通过向I方向旋转 角度来消除干涉点，但刀具系在旋转过程中有可能再与其他曲面特征点发生干涉。因此刀具系旋转后，必须计算新的刀轴矢量，并重新建立新的刀具坐标系，再进行与曲面的干涉检查。当干涉现象不能通过旋转刀轴方式消除时，则采用沿刀轴方向的抬刀方式来消除。

    2. 抬刀方式

    采用沿刀轴方向抬刀方式消除干涉时，应计算沿ZT方向的抬刀量。对于m个干涉点Pi(i=1，2，…，m)，计算每个干涉点排除的抬刀量 zi(i=1，2，…，m)，并同样取其中最大量为刀具抬刀量 z。

    如图6 所示，为环形刀加工时抬刀量的计算，有两种情况。当干涉点Pi落入半径为(R-R1)的刀具圆柱体S1内时，刀具向上抬刀，干涉点最后与刀具底平面相交，其抬刀量计算为

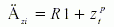    (12)

    当干涉点Pi落于半径差为R1的圆环体S2内时，抬刀时干涉点与刀刃圆弧面相交，其抬刀量为

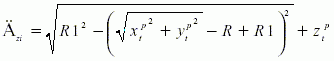    (13)

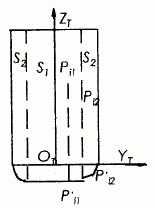
图6 干涉消除的抬刀量计算