1  前  言

    某厂 PG6531B型燃气轮机减速箱的齿轮材料为45CrNiMoVA。大齿轮（从动齿轮）齿数为121，转速为3 600r/min，小齿轮（主动齿轮）齿数为85，转速为5 100r/min。机组87年投用，2001年9月，机组超速螺栓动作，机组停车。对减速箱进行检查发现，主动轴与从动轴一对相啮合的大小齿轮发生严重崩齿损坏，造成齿轮副报废，机组瘫痪。该机组累计运行时间为70 000h。

    大齿轮和相啮合的高速轴小齿轮均发生严重断齿损坏，断裂部位均在齿根。大齿轮最为严重。断齿内侧在节线附近有约3~4mm的点状剥落带。宏观形貌呈现明显的双向贝纹线属于双向疲劳断裂，疲劳源在齿宽中部的齿根部位。为典型多源低周、延性疲劳断口。

    2  轮齿应力及材料分析

    齿轮相互啮合传动过程中，轮齿间产生滚动和滑动运动。轮齿表面和次表面金属承受拉伸、压缩和剪切应力这些应力用图1表示。在啮合传动过程中，轮齿表面承受不同形式应力作用，齿面和近表面金属在拉伸、压缩和剪切应力作用下，经多次重复应力作用，齿面和近表面金属可能产生微小裂纹形成疲劳源，随之应力循环次数增加，裂纹将扩展以致相互连接起来形成小块金属脱落，齿面出现点蚀剥落，齿轮齿面产生疲劳损坏。对断齿疲劳源附近取样作材料分析，结果表明，点蚀齿面近表面金属有多条疲劳裂纹，疲劳裂纹方向与表面呈45o。金相检查发现渗碳层组织粗大，无粒状碳氮化合物，残余奥氏体较多。齿面硬度偏低（HRC56）,促使齿轮抗接触疲劳性能降低。在重复应力作用下，经过高周次接触应力循环作用，微裂纹扩展及聚合。导致轮齿断裂。

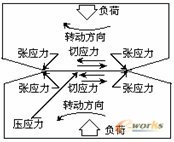
图1A  齿轮啮合时接触面间应力分布

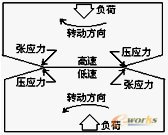
图1B  齿轮啮合时接触面间应力分布

    3  三维非线性有限元分析

    齿轮系统包括由齿轮副、传动轴组成的传动系统和由箱体和轴承组成的结构系统，存在着各种非线性耦合振动和非线性间隙冲击振动。为从运动学角度分析轮齿断裂原因，借助Ug以及ansys有限元软件，建立三维分析模型。

    3.1  齿轮传动冲击及动力接触有限元模型

    齿轮的间隙冲击以及啮入啮出冲击将对齿轮的动载荷和动态特性产生严重不良影响，齿轮间隙反应在动力学方程中是强非线性项，考虑传动误差、齿面摩擦以及时变刚度等实际因素。根据以下动力方程，建立模型，分析当存在齿轮初速冲击或突加载荷冲击时齿侧间隙对动态啮合力影响。

    两物体的冲击—动力接触问题的动力方程为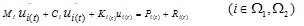
        
    式中Mi为i物体的质量矩阵；Ci为i物体的阻尼矩阵；Ki(t)为i物体的刚度矩阵；Pi(t)为i物体的载荷向量；Ri(t)为i物体的接触力向量；ui(t) 为i物体的位移向量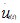；  为i物体的速度向量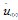； 为i物体的加速度向量。 

    采用NewMark—b法可以得到动力接触面上的有效柔度方程

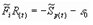
    式中: 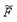   为接触面上的有效柔度矩阵;  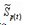    为有效外载荷在动力接触面上产生的接触点的相对间距；eo为接触点对原始间隙.

    由于Newmark—b直接积分法是针对连续介质提出的逐步积分公式，对于冲击动力接触问题在物体初始接触和初始分离时，由于接触压力发生突变，不满足Newmark—b  法关于加速度在t~t+D t区间线性变化的假设，必须采用加权平均法进行修正。

     3.2  齿轮间隙的影响分析
   
    图2为斜齿轮三维冲击—动力接触有限元分析模型。其几何参数为m=3.5，z1=85，z2=121，b=50mm，b =13.5°。对突加载荷冲击，初速冲击及啮入冲击下的齿轮传动动态特性进行了数值仿真，分析了齿轮间隙的影响。齿侧间隙对动态啮合力影响分析表明，轮齿突加载荷时，冲击接触时间与齿轮设计参数有关，与突加载荷大小无关；啮合轮齿越多，冲击力对时间的变化率越小；轮齿总啮入冲击力与初速及突加载荷成正比，随测隙增大，接触时间略有减少，总冲击力迅速增加。由此可见，传动齿轮的装配精度对轮齿使用寿命非常关键。