3.综合梁的优化设计 3.1 问题描述
如图所示的梁,长度L=1000mm,两端均为固定铰链约束(超静定),在距离右端1/5处作用集中载荷,利用ANSYS优化分析技术,确定最佳的宽、高的比,使得梁的总质量最小。梁的弹性模量E=2.0e5,泊松比0.3,初始的宽度W和高度H均为20mm,集中力F=1000N。应力的取值范围为:195-200pa;W、H的取值范围为:20-50mm
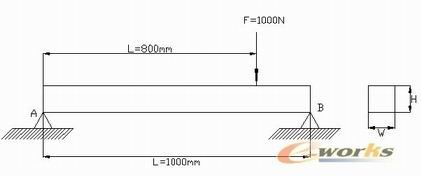
图5-13 两端铰支梁结构图
3.1.1 优化流程图如下所示:
1.输入长宽高的初始值、弹性模量和泊松比
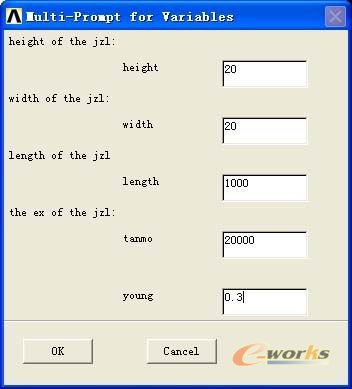
2 指定设计变量的范围:
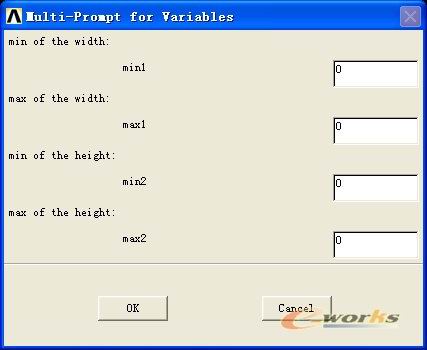
3.步指定状态变量的范围:
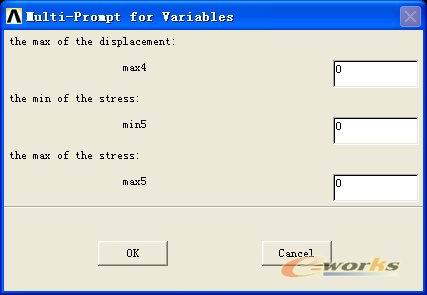
4 .进行优化
通过程序的运算,从结果中来看,该程序很好地实现了对该问题的优化,在满足设计条件下,结果所得的最佳的宽高比为0.91,节省材料为原材料的17.3%。
3.2问题描述
如图所示的悬臂梁,长度为1000mm,初始高度H=20mm,宽度W=20mm,作用均布载荷F=20N,宽度和高度的范围均为:10-50mm;极限应力为10000pa;最大的位移为0.2mm,利用ANSYS优化技术确定该梁最佳的宽高比,以及节省的材料的百分比。
弹性模量:E=30e6pa 泊松比:0.3
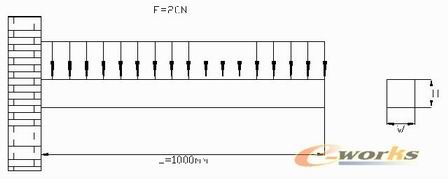
图5-18 悬臂梁结构图
3.2.1 优化结果
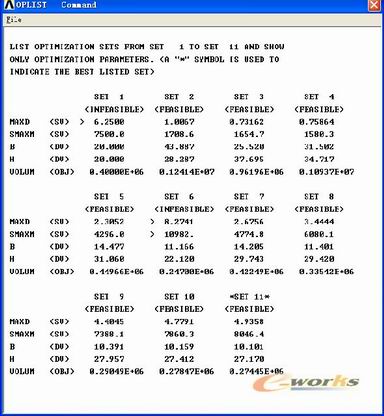
经过11次优化循环,得到了满足优化条件的设计序列如下图所示:
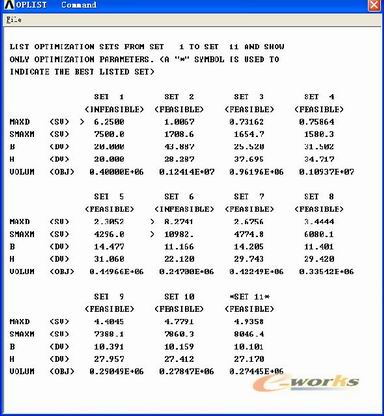
图5-19 所有优化设计序列
从以上的结果中可以看出满足条件的最佳的宽高比为:0.37,可以节省的材料百分比为:31.4%。
4.小结
以上实例的运算使用了作者自行编制的优化程序模块,从结果来看,基本实现了对矩形截面量在各种载荷条件下尺寸的优化。使用该程序可以实现的优化种类有:两端铰支(超静定)矩形梁在任何点作用集中力或在整个梁上作用分布力;一端固支的矩形梁在任何点作用集中力或整个梁上作用分布力等两类四种载荷梁的优化。该程序模块的优点是:1.采用交互式的操作界面使得优化过程操作简单化2.对于APDL用户来说该程序的有较灵活的修改特性。不足之处在于,程序中梁的截面形状必须是矩形的,再者程序中的优化设计变量状态变量的数目都是确定的,具体到实际应用中还需要做大量的工作。