式中 p—原岩应力。由式(1) 可见, 在r=5a的地方, 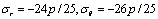 , 两者均已接近原岩应力。此处开挖小孔的影响已衰减到4%,可将其视为影响的最大边界,在边界以外即为原岩应力场,因此可取模型的三维尺寸为:
, 两者均已接近原岩应力。此处开挖小孔的影响已衰减到4%,可将其视为影响的最大边界,在边界以外即为原岩应力场,因此可取模型的三维尺寸为: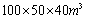 。
。 3.3 模型边界条件与荷载模式
模型侧面和底面为限制位移边界,模型上表面为地表,取为自由边界,作用有均布压力1.4MPa。模型剖面如图1所示:
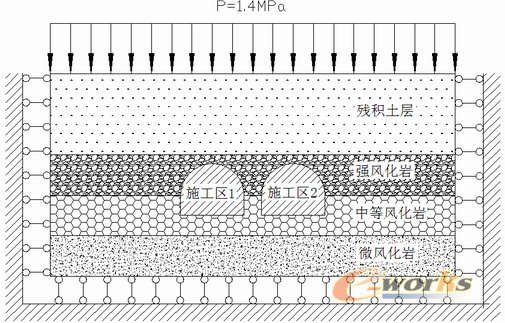
图1计算模型
土层分类及其性质如表1所示:

表1土层分布及性质
4.计算及结果分析
本次数值模拟使用FLAC3D对地下隧道开挖的两种施工方式施工全过程进行了仿真,具体施工顺序如框图4所示,三维模型的建立和动态施工过程是通过编程来实现的,通过提高围岩的物理力学参数来模拟喷射混凝土,通过SHELL构件来模拟内部结构支护。
4.1计算说明
两种施工方式计算模型如图2、3所示,模型1为“两导洞”法计算模型,模型2为 “三导洞”法计算模型。模型1单元数大约为16000个,模型2单元数约为20000个,初始平衡率为5E-5,每进行一步开挖计算1000steps,按 10m/d的进度开挖,计算总时间约为10小时。历史记录点取自与洞室垂直的地表,分别沿纵向和横向每隔5米布置一个监测点并记录位移值。
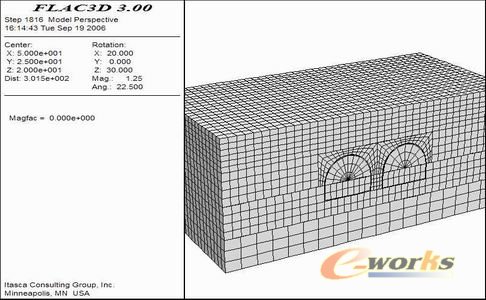
图2模型1
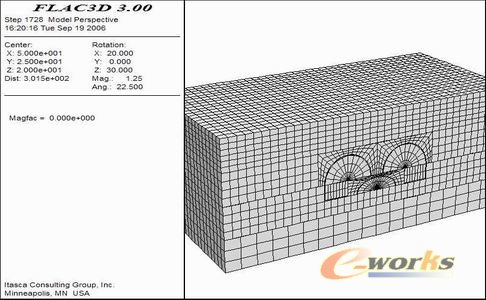
图3模型 2
初次支护采用喷射混凝土支护,二次支护采用壳单元结构支护,具体参数如表2 所示:

表2支护参数表
程序计算过程依据如下实际施工步骤图:
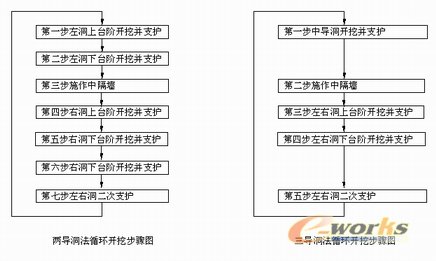
图4 施工步骤图
4.2 结果分析
两种工法施工完成时Z方向位移等值线图如图5、6所示。

图5 模型1 Z向等值线图

图6模型2 Z向等值线图
两种工法地表沉降曲线如图7、8所示,其中系列1为左洞地表沉降曲线,系列2为右洞地表沉降曲线,系列3为中间地表沉降曲线。
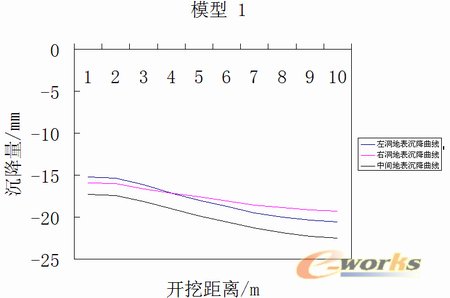
图7模型1 地表沉降曲线图
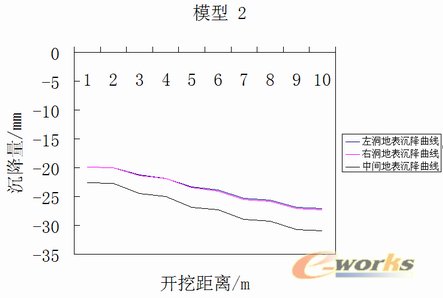
图8 模型2地表沉降曲线
通过计算得出两种工法的最大沉降量点均在中间地表,最大沉降量对比如图9所示。
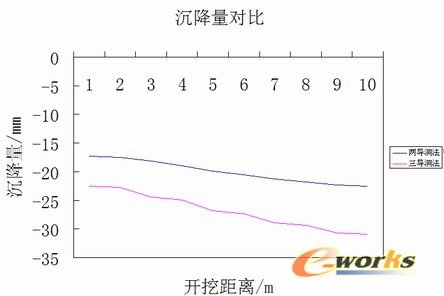
图9 两种施工方法比较
通过以上计算及两种施工方法最大沉降量曲线对比可以得出如下结论:
(1)“两导洞”法由于施工的先后顺序使得左右两洞地表的沉降量体现出一定的差异;“三导洞”法采用对称施工法,左右两洞的沉降量基本一致,这与实际情况基本相符。
(2)“两导洞”法施工过程中,中间墙体是主要受力部分,因此在左洞室施工过程中应该加强中间墙的支护。
(3)“三导洞”法施工过程中,中间临时支护是关键,在拆除过程中容易造成隧道边角和拱角处应力过大破坏,应该做好预防措施。
(4)“两导洞”最大沉降量22.52mm,“三导洞”法最大沉降量30.9mm。由于施工顺序的差别两种沉降曲线略有不同,这主要是由于不同施工方式引起应力分布的不均造成的。
(5)通过两种施工方法最大沉降曲线对比可知,此次数值模拟中,“两导洞”所得到的结果较为理想。