第一十六章 接触分析

16.5.1  工程背景

在汽车、航空、家电等工业部门 ,许多构件是用板料冲压成形生产的。板料成形过程牵涉到几何非线性、材料非线性和边界条件非线性的复杂的力学问题。金属板料冲压成型利用金属塑性变形的特点，通过对金属板料施加压力，使其产生塑性变形，从而获得所需要的形状。由于板料冲压成型过程包含大位移、大变形等十分复杂的物理现象，使得对其成型控制非常困难，以前更多的是通过反复试验的方法制造出合乎要求的产品，其过程需要花费大量的时间和经费。随着有限元模拟技术的迅速发展，利用有限元软件模拟金属板料冲压成型过程及分析其回弹量已成为可能。本实例使用ANSYS模拟薄钢板的冲压分析。

16.5.2 问题的描述

1．模型的几何尺寸

本实例假设薄钢板两个方向的尺寸远大于厚度，因此可以简化为平面应变问题，又因为平面模型的左右对称性，所以只需建立平面的1/2模型，其力学模型简图如图16-22所示。图中给出了基本的模型尺寸，且薄钢板的半长为L，薄钢板的厚度为 ，L2和L1之间存在以下关系：L2=L1+H，表16-1给出了模型的基本数据。

表16-1 模型的基本几何尺寸

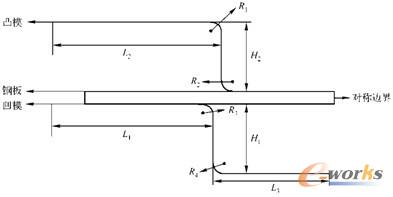
图16-22  薄板冲压的模型简图

2．单元的选择及材料常数

因为冲压是大变形、塑性，所以本实例选用4节点平面单元PLANE42，并通过设置关键字K3实现模拟平面应变问题。凸模和凹模假设为刚性材料，通过接触向导来实现对其的定义；钢板的应力应变关系假设为双线性等向强化，各材料参数分别为弹性模型为2E11Pa，泊松比为0.3，屈服强度为200MPa，切线模量为2E9Pa，其应力应变关系如图16-23所示。

3．边界条件

本实例假设整个冲压过程为准静态，即为静力学分析并且步考虑温度的影响。固定凹模的所有自由度，在凸上约束X平移自由度和转动自由度，在凸模上施加Y方向的位移为-H1；约束薄钢板的右端面为对称约束，冲压接触后再施加Y方向位移为0.2×H2。

图16-23  薄钢板的应力应变关系曲线