第八章 代数方程和常微分方程求解

符号绘图函数fplot()和ezplot()也可以用于图解法求代数方程的根，它适用于求解维数较少的一维方程或二维方程组。
对于一维方程图解，其解就是函数曲线与x轴交点所对应的变量数值。如果有多个交点，则表示该方程有多个解；如果没有交点，则表示该方程没有解。
例如，在例5-3使用符号绘图函数绘制代数方程的图形（图5-3左图）中可见，函数在区间[-5,5]内与x轴有3个交点，因此该代数方程该区间内有3个实根。
对于二维方程组图解，其解就是两条函数曲线的交点所对应的坐标数值。如果只有1个交点（或切点），则表示该方程组有1个解；如果有两个交点，则表示该方程组有两个解；如果没有交点，则表示该方程没有解。

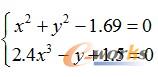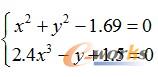例8-1  用图解法求解二维联立方程的图解。
a=-2;b=2;                                         % 定义横轴区间
ezplot('x^2+y^2?1.69',[a,b]);                      % 符号函数1绘图
axis 'equal';                                      % 控制坐标轴比例相等
hold on;grid on;
ezplot('2.4*x^3?y+1.5',[a,b]);                     % 符号函数2绘图
line([a,b],[0,0]);                                 % 绘制横轴
line([0,0],[b,a]);                                 % 绘制纵轴
xlabel('\bf x');ylabel('\bf y');
title('\bf 二维代数方程组的图解法')
gtext('\bf f_1=x^2+y^2?1.3^2');
gtext('\bf f_2=2.4x^3?y+1.5');
gtext('\bf (x_1,y_1)');gtext('\bf (x_2,y_2)');
M文件运行结果如图8-1所示。从此图中可见，由于该二维联立方程曲线有两个交点，所以有两对实根。

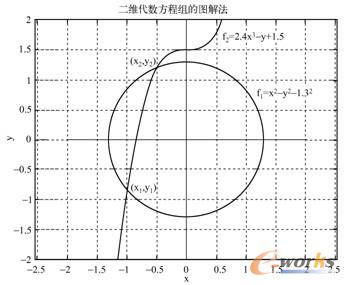
图8-1  二维代数方程组图解法