第九章 最优化问题和遗传算法

1．一维无约束优化的遗传算法
例9-8  采用遗传算法求解一维函数

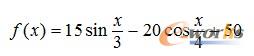
在x∈（0，80）范围内，求f（x）取最大值时的自变量x值。
（1）使用优化工具箱中优化函数fmincon进行计算
% 定义函数和变量
f=inline('15*sin(x/3)-20*cos(x/4)+50','x');
% 使用优化函数fmincon计算
for x0=[0:2:80,0:4:80]                     % 任意选择初值
    x=fmincon(f,x0,[],[],[],[],0,80);       % 非线性约束优化
    xf=[[];x0,x,f(x)];
end

M文件运行结果
Optimization terminated: magnitude of directional derivative in search
 direction less than 2*options.TolFun and maximum constraint violation
  is less than options.TolCon.
No active inequalities.
可见，在求解区间内任意选择初值，并不能得到满意的结果。
（2）绘制一维非线性函数曲线
% 绘制函数曲线
figure(1);
fplot('15*sin(x/3)-20*cos(x/4)+50',[0,80])
xlabel('\bf x');ylabel('\bf f(x)');
gtext('\bf f(x)=15sin(x/3)-20cos(x/4)+50');
grid; hold on;
M文件运行的结果如图9-4所示。

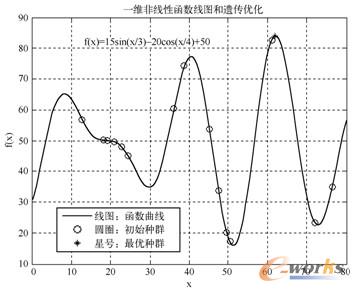
图9-4 一维非线性函数线图和遗传优化

从图9-4可见，一维非线性函数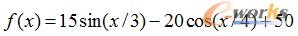的图形是一条振荡曲线，在解区间[0,80]内有多个极值点。
（3）采用遗传优化算法求解
1）定义适应度。
% 定义适应度函数文件
function [sol,y]=maxf_1(sol,options)
x=sol(1);
y=15*sin(x/3)-20*cos(x/4)+50;
2）生成初始种群，个体数目取15。
% 生成初始种群，个体数目取15
startPop=initializega(15,[0,80],'maxf_1')
% 在图中以绿色“o”号标示初始种群
plot(startPop(:,1),startPop(:,2),'go');
title('\bf 一维非线性函数线图和初始种群及遗传优化')
M文件运行随机生成的初始种群是：
startPop =
   38.6805   74.2211
   18.0454   50.0209
   24.3110   44.9555
   50.2384   17.0784
   19.3034   49.9962
   71.9443   23.3046
   22.6353   48.0634
   60.9747   82.8144
   49.4000   20.1467
   76.3021   34.9598
   45.1242   53.6422
   36.0381   60.4131
   20.9398   49.6439
   47.3629   33.8447
   12.6614   56.7730
3）调用遗传优化算法函数，取进化繁殖100代，变异概率为0.08，浮点编码。
% 遗传优化算法搜索
[xf,endPop,bPop,trace]=ga([0,80],'maxf_1',[],startPop,[1e-6 1 1], 'maxGenterm',
100,'normGeomSelect',[0.08],['arithXover'],[2],'nonUnifMutation',[2 100 3]);
xf
% 在图中以红色“*”号标示最优种群
plot(endPop(:,1),endPop(:,2),'r*');
Legend('圆圈：初始种群','星号：最优种群')
M文件运行后，最优种群的星号标记在图9-4中，计算结果如表9-2所示。

表9-2 遗传算法搜索的中间结果

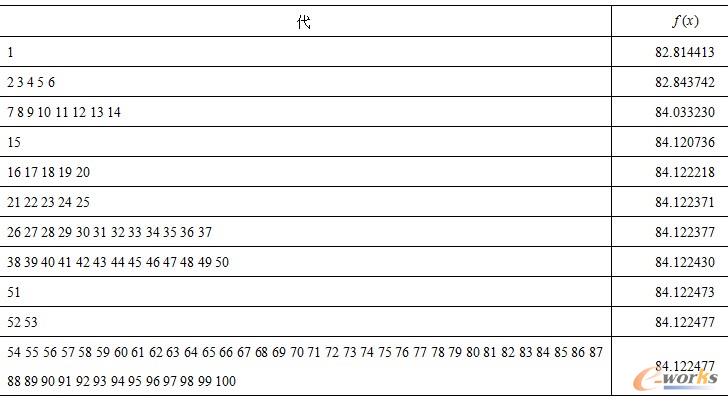
从表9-2可见，从第52代开始，就可以得到较精确的结果。经过100代搜索，获得最优种群及其函数值是：
xf =
   61.9343   84.1225
即 ， 。
（4）描述遗传算法搜索过程。
% 每一代中的最好解与平均值
figure(2);
plot(trace(:,1),trace(:,2),'b:');
hold on;
plot(trace(:,1),trace(:,3),'r');
grid;
xlabel('\bf Generation');ylabel('\bf Fitness');
title('\bf 一维非线性遗传算法的各代最优解与平均值');
legend('虚线：各代种群平均值','实线：各代最优解')
M文件运行的结果如图9-5所示，图中实线表示各代最优解，虚线表示各代种群平均值。

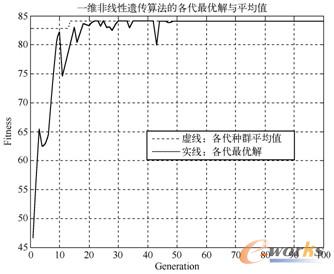
图9-5 一维非线性遗传算法的各代最优解与平均值

2．多维无约束优化的遗传算法
例9-9 采用遗传算法求解二维非线性优化问题

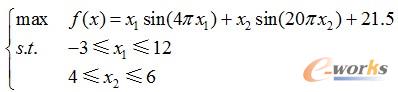
（1）绘制二维非线性函数图形
% 绘制二维非线性函数图形
x=linspace(-3,12,35);y=linspace(4,6,15);
[x1,x2]=meshgrid(x,y);
f=x1.*sin(4*pi*x1)+x2.*sin(20*pi.*x2)+21.5;          % 目标函数
surf(x1,x2,f)
xlabel('\bf x_1');ylabel('\bf x_2');zlabel('\bf f(x_1,x_2)')
title('\bf f(x_1,x_2)=x_1sin(4\pix_1)+x_2sin(20\pix_2)+21.5')
M文件运行的结果如图9-6所示。

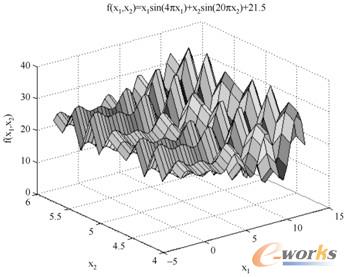
图9-6  二维非线性函数图形

（2）定义适应度函数
% 定义适应度函数文件
function [sol,y]=minf_2(sol,options)
x(1)=sol(1);x(2)=sol(2);
y=x(1).*sin(4*pi.*x(1))+x(2).*sin(20*pi.*x(2))+21.5;
（3）生成初始种群
% 生成初始种群，个体数目取10
bounds=[-3 12;4 6];                                  % 变量上下限
initPop=initializega(10,bounds,'minf_2');
（4）采用遗传优化算法求解，进化繁殖200代，其他为默认参数
% 遗传优化算法搜索
[xf,endPop,beestSols,trace]=ga(bounds,'minf_2',[],[],[],'maxGenTerm',200);
beestSols
xf
M文件运行结果是：
beestSols =
    1.0000    8.6129    5.8287   35.6853
    3.0000   10.6648    5.6254   36.4818
    4.0000   11.6428    5.8287   38.5248
   15.0000   11.6343    5.8287   38.7274
   16.0000   11.6277    5.8287   38.7931
   17.0000   11.6343    5.9274   38.9171
   19.0000   11.6277    5.9274   38.9831
   23.0000   11.6277    5.9233   39.0102
   25.0000   11.6277    5.9252   39.0455
   28.0000   11.6277    5.9251   39.0458
   29.0000   11.6277    5.9250   39.0458
   48.0000   11.6271    5.9250   39.0481
   50.0000   11.6270    5.9250   39.0485
   51.0000   11.6269    5.9250   39.0487
   53.0000   11.6268    5.9250   39.0489
   55.0000   11.6267    5.9250   39.0490
   56.0000   11.6267    5.9250   39.0492
   63.0000   11.6262    5.9250   39.0499
   64.0000   11.6261    5.9250   39.0500
   65.0000   11.6260    5.9250   39.0501
   67.0000   11.6257    5.9250   39.0503
   69.0000   11.6255    5.9250   39.0503
   91.0000   11.6256    5.9250   39.0503
   93.0000   11.6256    5.9250   39.0503
  200.0000   11.6255    5.9250   39.0503
xf =
   11.6255    5.9250   39.0503
运算结果表明，繁殖到第67代时获得最优解

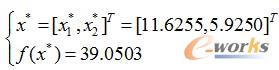
（5）描述遗传算法搜索过程
plot(trace(:,1),trace(:,2),'b:');
hold on;
plot(trace(:,1),trace(:,3),'r');
grid;
xlabel('\bf Generation');ylabel('\bf Fitness');
title('\bf 二维非线性遗传算法的各代最优解与平均值');
legend('虚线：各代种群平均值','实线：各代最优解')
M文件运行结果如图9-7所示，图中实线表示各代最优解，虚线表示各代种群平均值。

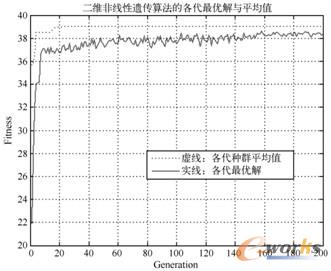
图9-7  二维非线性遗传算法的各代最优解与平均值