在采用数控机床加工零件时，往往会遇到零件形状是由复杂的空间曲线构成。已知条件是曲线的方程，这些方程可能是直接得到的，或者是通过轮廓形状上的一些关键点，通过拟合的方法得到近似的曲线方程。特别在起重机、锅炉制造等行业经常有不同管径的圆管交叉连接。其中两管相贯线的确定和精确切割加工是一个难点。常用的方法是在知道管的相对位置等条件下，经过计算手工制出模板，用模板画线，手工切割。其过程十分烦琐，且切割精度也无法保证。数控加工的目的在于按照已知的曲线方程加工零件，因此将曲线转换为数控加工需要的数控代码是很重要的一个环节。

    如果用手工编程，则效率低、可靠性差，不能充分发挥机床的功能和性能。随着CAD/CAM技术的发展，国外许多高档的CAD软件都具有相应的CAM模块。例如美国SRDC公司的I_DEAS、PTC公司的Pro/E、UG、SolidWork等性能良好的CAM模块。利用其三维实体数据生成数控加工代码，通过通讯接口传输到数控机床的数控系统。也有一些第三方开发的CAM模块，可与CAD软件无缝集成，完成数控代码的生成。然而，这些软件相对来说要求高，价格昂贵。且没有配置专用的后置处理器，或者只配置了通用的后置处理器而没有根据数控机床的特点进行二次开发，由此产生的代码还需要做大量的手工修改。

    本文以Autodesk公司的AutoCAD2000为平台,利用其内嵌的ARX编程工具，针对生产现场的数控切割机床加工两管的相贯线，开发了一套能够计算并自动获得相贯线数控加工代码的系统。通过设置刀具路径等工艺参数和后置处理，最后生成NC代码，供数控机床加工零件。此过程可以节省大量的人力和时间。并且最大限度的减少人为和系统因素的影响，使管缝切割精度高，保证焊接质量更加稳定可靠。在一定程度上弥补了零件制造从设计到成型的薄弱环节。

    1.数学模型的建立

    两个圆管的相交形式多样。但都是两个相同或者不同直径的圆柱面以一定的角度相交形成的空间曲线。如图1所示。

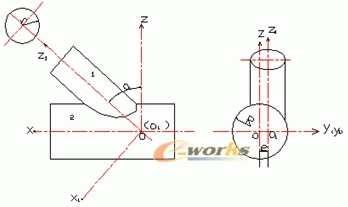
图 1

    圆柱面(1)的参数方程表示为：

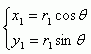
    圆柱面(2)的参数方程表示为：

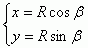
    两个坐标的变换式：

    两圆柱面的相交轨迹即为相贯线，相贯线是一条复杂的空间曲线，在o-xyz空间内其方程为可以表示为:

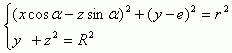
    转换到极坐标下的表示为:

    同理可以求得在 空间内的相贯线的方程

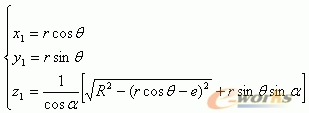
    通过以上的数学推导，可以得到相贯线的解析式。上式是相贯线精确的数学表达式，可以根据任意精度要求来取值，满足数控系统实时加工的要求。通过公式可以求得空间曲线上每一点的坐标值。