1 前言

    由于蠕变试验费时费力，而且不能体现设备运行的各种工况。因此,有限元数值模拟具有简单、快速、经济等特点，在工程中得到广泛的应用。ANSYS在模拟金属材料的蠕变时，对蠕变的第一阶段和第二阶段可获得令人满意的结果，而对蠕变的第三阶段模拟尚未有合适的模型。ANSYS用户编程特性（UPFs），能满足用户的特殊需要，允许用户将自己的FORTRAN程序连接到ANSYS中，是ANSYS的非标准应用。本文运用ANSYS 5.7的二次开发功能，将含有损伤的蠕变模型写入ANSYS，模拟了单轴与多轴应力状态下P91钢的蠕变全过程，对高温金属蠕变进行研究，并对多轴应力状态下弯头发生蠕变变形进行分析，指出蠕变效应对弯头部位应力变化的影响，通过对骨点应力（Skeletal Point Stress）的分析，指出弯头部件蠕变损耗的变化情况。为正确预测在多轴应力状态下高温部件蠕变寿命提供了理论依据，对于评估高温构件的安全性和经济性具有十分重要的应用价值。

2 蠕变方程

    经过大量实验研究表明，金属材料在蠕变过程中，会发生硬化和弱化现象，根据文献[1,2]，建构损伤-硬化蠕变模型，并假定材料的损伤是产生在蠕变的第三阶段。该蠕变模型由两部分构成：一是材料的硬化部分，二是材料的损伤部分。蠕变损伤-硬化模型形式如下：

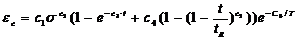（1）

    式中， ε_c为蠕变应变；σ为应力；t为蠕变时间；t_R为蠕变断裂时间； T为绝对温度；c₁、c₂、c₃、c₆为材料常数；c₄、c₅、t_R为应力σ的函数。

    应用式（1）本构方程对文献[3]中P91钢的实验数据进行数值模拟验证。图1为单轴应力状态下的公式计算和模拟结果，图2 为多轴应力状态下的模拟结果。由单轴及多轴蠕变模拟结果可知，通过UPFs用损伤-硬化蠕变模型可以模拟多轴应力状态下蠕变全过程。

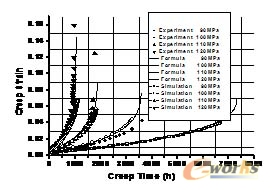
图1 光滑试棒实验与ANSYS模拟结果 

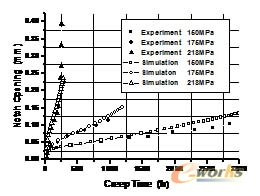
图2 缺口试棒开口变化量实验与ANSYS模拟结果

3 骨点（Skeletal Point）等效应力

    在多轴应力状态下，材料损伤与应力应变状态的关系非常复杂。一般认为，应力状态对损伤的累积主要有两个方面的影响，一是不同的应力对损伤率的贡献不同，损伤率应由等效应力（当量应力）确定，其次为多轴的约束作用影响了韧性，约束度越大则韧性越差^[4]。因此，对于多轴应力状态下提出使用等效应力对材料的蠕变进行计算。

    假定等效应力采用下式形式

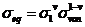（2）

    其中，σ_eq－等效应力；σ₁－第一主应力；σ_von－Von Misses应力；v－材料常数，可以通过蠕变试验来确定，此处取0.072。

    图3、图4、图5是在名义应力分别为164.31MPa，191.69MPa，238.81MPa时，对文献[1] 中的缺口试棒的ANSYS数值模拟结果，图为缺口喉部等效应力沿半径的变化曲线。

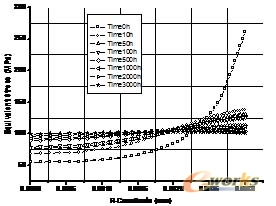
图3 不同时刻等效应力沿喉部半径的分布

 σ_net＝164.31MPa

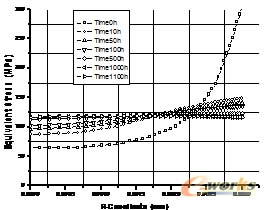
图4 不同时刻等效应力沿喉部半径的分布

 σ_net＝191.69MPa

图5 不同时刻等效应力沿喉部半径的分布

 σ_net＝238.81MPa