虚节点法优点如下:
1) 它继承了运动边界法的优点,未改变刚度矩阵的带宽,保证了刚度矩阵的对称性和正定性,保证了对大型方程组求解过程中的收敛和精度。
2) 转子模型无需旋转,使有限元前处理过程大大简化。省去了用循环程序计算相绕组反电势和计算电磁转矩等时对转子模型的旋转和重新划分网格。转子上的永磁体的材料属性无需随相对坐标系的旋转而变化,也无需重新划分网格。这样在上百次的计算中,可大量节省计算时间。
虚节点法仍存在一些缺点:
1) 后处理中图形在运动边界两侧的区域显示不连续,但不影响计算结果。
2) 和运动边界法一样,仍然属于固定空间步长法,不能处理转子旋转到任意位置时情况,因而不便于处理电机暂态起动问题,通用性不好。
2.4 用拉格朗日插值法处理运动边界
在处理电机稳态问题(转子不动或匀速旋转)时,可方便的使用上述虚节点法,其实质是空间固定步长法。对运动边界分网时,沿径向网格单元的长度所对应的圆心角即为转子旋转的最小旋转圆心角,转动时旋转步长只能取气隙中有限元网格单元边长的整数倍。这样的处理方法由于网格单元长度的限制,不允许转子旋转任意角度,否则定转子运动边界上的节点不重合,如图6所示,认为此情况下有限元模型不连续,不能形成模型整体的刚度矩阵。
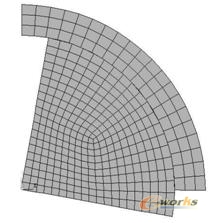
图6 定转子运动边界上的节点不重合
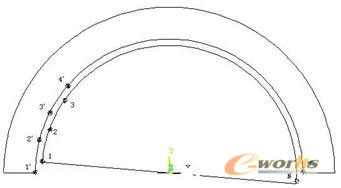
图7 转子模型旋转任意角度时定转子相对位置
但有很多实际问题如电动机的暂态起动问题,由于起动过程转速变化范围较大,转速从零开始逐渐加速直到额定转速,无法做到每次处理运动边界时按照空间固定步长法,即每次计算都让运动边界上的节点重合,如图7所示。当转速为0.1rad/s时,此时时间步长取0.001s,转子转动的空间角度将不超过0.0001rad。此时如果采取保持空间步长为定常数,而调整时间步长的策略,势必需将运动边界分网时使用非常稠密的网格,才能按虚节点法处理,但如此会使有限元模型中单元数量庞大,占用大量计算资源,使计算周期很长,甚至有可能不能计算。因此虚节点法不能直接适用于电机起动等转速变化大的暂态分析计算。
数值计算方法中的拉格朗日插值法非常适用于解决此类问题。通过插值方法,即可取消运动边界上节点必须一一对齐的约束条件。我们所熟知的拉格朗日插值法中有两点一次线性插值法和三点二次抛物线插值法,前者计算简单,但计算精度低于后者,这里主要介绍线性插值法,因为线性插值法的精度已经满足计算要求了,读者可自己尝试用三点二次抛物线插值法。虽然定转子运动边界不重合时,运动边界上所有节点都要使用线性插值法,但因为运动边界剖分时被均分为(N-1)段,因而每一节点所用的插值基函数都相同,为简化带来方便。设在t0时刻,定转子模型相对位置见图1,节点1与1’耦合,2与2’耦合,依此类推,N与N’耦合。令圆弧1’ 2’的弧长为沿径向运动边界上网格的最短单元长度。经过一个时间步长即t1时刻,定转子模型相对位置见图7,节点2’位于节点1和节点 2所构成的单元边上。运用线性插值法建立上述情况运动边界上节点磁位的耦合,节点2’的磁位可用点1、2的磁位表示,详见公式(2)。
A2’=K1A1+K2A2 (2)
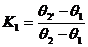 ,
, 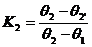
其中K1、K2为插值基函数,A1、A2、A2’、θ1、θ2、θ2’分别为节点1、2和2’的磁位和电角度。
用APDL实现过程中的具体思路如下。当转子瞬时转速为ω(τ)时,转子在任意时刻的旋转角度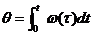 ,只考虑转子旋转一个磁极范围。转子运动边界一个极距范围对应180°电角度,假设将运动边界平均分为(N-1)段,即有N个节点,则运动边界每小段对应的电角度β=180/(N-1)。则对应转子在任意时刻的旋转角度θ,转子转过的虚节点数为λ=INT(θ/β)。
,只考虑转子旋转一个磁极范围。转子运动边界一个极距范围对应180°电角度,假设将运动边界平均分为(N-1)段,即有N个节点,则运动边界每小段对应的电角度β=180/(N-1)。则对应转子在任意时刻的旋转角度θ,转子转过的虚节点数为λ=INT(θ/β)。