事先定义两个数组delt(1),delt(2),分别存放定子和转子运动边界节点编号,并保存,这样每次调入模型,取节点号码时,就不用重新选取节点了,把常用的数据做成数组存储起来,可节省计算时间。
耦合定转子运动边界节点的磁位。用上述转子运动边界虚节点法的耦合节点规律,以图7说明。当转子转过的虚节点数为λ时(λ从0取到(N-1)),满足插值方程A2’=K1A1+K2A2,依此类推。
2.5 计算结果
图8、9、10、11是一永磁电机的计算结果。从图8和图9中电机局部磁力线分布可见,用转子运动边界虚节点法处理后,后处理结果显示时在定转子气隙中有磁力线不连续现象。

图8 (定转子按运动边界法)局部磁力线分布
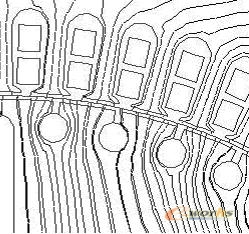
图9 (转子运动边界虚节点法)局部磁力线分布
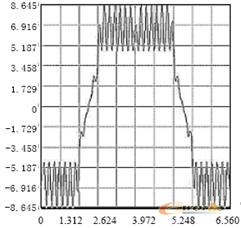
图10 气隙磁密切向分量波形
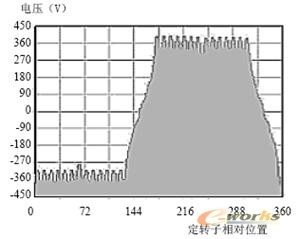
图11 一相绕组的空载反电势波形
3 结论
经过这样处理后,解决了时步有限元方法中时间步长难于处理的困难。在处理运动边界问题时,完全可以选取时间步长为定常数,在不增加运动边界节点和计算工作量情况下,有效的保证转子可在一个时间步长中旋转任意角度,而且可以提供很好的计算精度。综合运用拉格朗日插值法与虚节点法成为更好的运动边界处理方法,此方法对电机稳态和暂态计算均适用。运用此方法由于在上百次循环计算过程中,只进行一次模型有限元剖分即可,大大简化编程,简化模型网格规模,可灵活的选择计算时间步长,并且在与运动边界法网格一致情况下,保证结果的计算精度相同,极大的节省宝贵的计算资源和计算时间,具有很好的通用性,适用于大部分电机运动边界的处理。
[参考文献]
【1】 孙玉田、杨明、李北芳 电机动态有限元法中的运动问题大电机技术 1997,(6)
【2】 严登俊、刘瑞芳、胡敏强、韩敬东 处理电磁场有限元运动问题的新方法中国电机工程学报 2003,(8)
【3】 汤蕴璆 电机内电磁场(第二版) 科技出版社,1998
【4】 倪光正 工程电磁场分析计算
【5】 李红 数值分析(第二版) 华中科技大学出版社,2004
【6】 ANSYS电磁场培训手册 成都办事处,2002
【7】 ANSYS APDL培训手册 成都办事处,2002