1  前言

    有限元法是目前电气工程中解决电磁场边值问题的重要手段，在工程中获得了广泛的应用。但目前对场域内介质间的相对运动问题的处理仍然值得我们去深入研究，如旋转电机中转子相对定子的运动模拟。研究电机暂态问题的最有效方法之一便是时步有限元方法，但目前的时步有限元法在处理定转子之间相对运动问题时，存在前处理程序复杂，对网格单元密度要求较高，计算效率低花费时间长，低速时时间步长较大等问题。针对上述问题，本文运用数值计算方法中拉格朗日插值法及转子运动边界虚节点法处理定转子的运动边界，提出一种新的处理方法，在新方法中定转子模型无需相对旋转，而且可模拟处理定转子模型相对旋转到任意位置时的情况。这样新方法中不再受运动边界节点必须对齐的约束，可设定时间步长为常数，空间步长由计算结果决定，对分析区域运动边界上节点的磁位建立耦合方程，获得模型在任意时刻的整体刚度矩阵，从而得到整个分析区域的离散解。

2  电磁场分析中处理运动边界的新方法

2.1 描述介质相对运动的电磁场的边值方程

    一切存在介质相对运动的电磁场都满足如下边值方程：

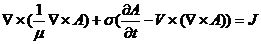       （1）

    式中A代表磁场的矢量磁位；V代表介质相对参考坐标系的运动速度；J代表外部强加的源电流密度；σ是介质的电导率。

    对（1）式进行离散时，将速度因子V带入刚度矩阵的处理方法显然不足取，因为这样将增加矢量磁位A对空间坐标的偏导数，不利于方程的离散及求解。

2.2  独立坐标系法（运动边界法）

    独立坐标系法，将电机气隙沿其径向中心线一分为二，在中心线上画两条完全重合的圆弧分别构成静止的定子边界和运动的转子边界。对定子和转子采用两套相对独立的坐标系，定子坐标系是固定在定子上的静止坐标系；转子坐标系固定在转子上，随转子以转子实际转速旋转。两个坐标系下的场是独立的，只通过气隙中心线上的节点进行周期性或半周期性边界条件的处理。定转子初始位置如图1所示，为方便看图，定转子之间留有一个空隙，其实模型中定转子边界是重合在一起的。让转子边界上的节点和定子边界上的对应节点耦合，即节点1与1’ 耦合，2与2’ 耦合，依此类推，N与N’ 耦合。其实建模时定转子分别建模，把重合的节点压缩（Merge）后，ANSYS程序自动满足。

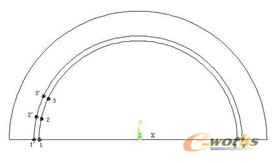
      图1定转子模型初始位置

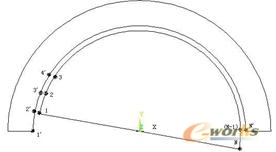
  图2定转子模型第一次旋转后相对位置

    假设转子沿顺时针方向匀速旋转，其每次旋转转过的圆心角均相等（即为圆弧12对应的圆心角）。图2所示为转子经过第一次旋转后定转子模型的相对位置。按如下规律耦合定转子边界上节点：对旋转后重合边界上的节点如1与2’ 耦合，2与3’ 耦合，依此类推；对转子运动边界上超出电机定子模型范围的节点按周期性或半周期性边界条件耦合如N与1’耦合，依此类推。

2.3  用转子运动边界虚节点法处理定转子的运动边界

    受运动边界法启发，如果不旋转转子模型，而按照上述运动边界法中耦合定转子边界上节点的规律，只对运动边界上的节点进行耦合，就可以产生一种新的处理方法――转子运动边界虚节点法，以下简称虚节点法。引入虚节点的概念，让模型不旋转，而设想转子运动边界上节点旋转到图2所示的空间位置，成为与计算无关的虚拟节点。该法仍将电机气隙沿其径向的中心线一分为二，画两条完全重合的圆弧分别构成定子边界和转子边界。但与运动边界法不同的是，定转子的有限元模型无需旋转，直接按运动后的情况耦合转子运动边界上的虚节点和定子运动边界上的节点。运动边界法的实质是耦合运动之后定转子运动边界上的节点，因而从本质上看虚节点法与运动边界法是相同的。图4为一永磁电机定转子一个磁极范围模型。图5为在定子上把转子旋转后对应的部分的模型也假设补充上。仍假设转子沿顺时针方向旋转，定子模型中面ABCD和面A’B’C’D’满足半周期对称边界条件，边AB与A’B’上对应节点的磁位值大小相等，符号相反。对转子运动边界上的虚节点与定子运动边界上的节点做如下处理，属重合边界上的节点如1与2’ 耦合，2与3’ 耦合，依此类推；对转子运动边界上超出电机定子模型范围的虚节点按半周期性边界条件耦合如N与1’耦合，依此类推。这样处理后定转子运动边界上的节点的耦合情况与运动边界法中的完全相同，区别仅是相对坐标系的旋转与否，但对结果的精度无影响。试想图1中模型的计算结果和把图1中定转子模型同时旋转一个角度后的计算结果一定完全相同，只是建模时的参考角度不同罢了。

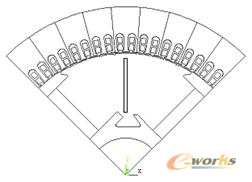
    图4转子模型旋转任意角度时定转子相对位置 

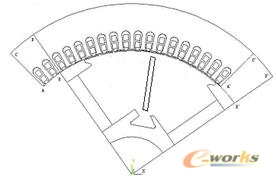
图5转子模型旋转固定空间步长时定转子相对位置