2.3边界条件与载荷工况

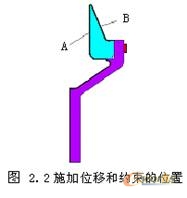
    本文研究重点是对比螺栓连接结构在不同边界处理方式下应力、变形情况，数学模型中省略了与结构1（图2.2）连接的其它部件。各种边界处理方式下结构均受到12.0MPa的压力载荷，载荷施加于如图2.2面组A上；约束了结构1与其它部件相粘接的面组B上所有自由度以限制其刚体位移；同时，由于模型的轴对称特性，在对称面上施加了对称约束；对于需要考虑螺栓与结构1、结构2的接触关系的区域建立了接触对。接触计算中，接触算法为增强的拉格朗日方法，接触探测为高斯积分点，计算中摩擦系数μ取值为0.2。

2.4材料特性

    由于材料参数对螺栓连接结构应力、变形情况的影响不是本文的研究重点。在应用ANSYS软件进行数值分析过程中，均采用线弹性本构关系来描述材料行为。

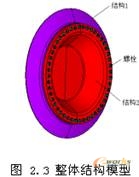
    假设螺栓与结构1（见图2.3）具有相同的材料属性，材料为30CrMnSiA，材料属性为：

    弹性模量  E =196GPa

    泊 松 比  μ=0.3

    结构2（见图2.3）采用了铝合金材料，材料属性为：

    弹性模量  E =71GPa

    泊 松 比  μ=0.33

2.5几何模型

    螺栓连接结构如图2.3由于结构为回转体，为节省计算机时间，在计算分析过程中截取了整体模型的四十八分之一（仅包含一个螺栓），如图2.4按照螺栓连接结构的不同边界处理方式，分别建立了三维几何模型。

2.5.1不考虑接触关系的几何模型

    建模时采取了以下两种简化方式对螺栓连接结构的边界进行处理：

    模型一：建立了如图2.4A所示的结构模型，不对螺栓进行建模，模型中仅包括结构1和结构2，并将二者利用耦合关键点的方式连接为一体。

    模型二：建立了如图2.4B所示的螺栓模型。虽然建立了螺栓模型，但不考虑螺栓与其它连接件的接触关系，将结构1、结构2与螺栓利用耦合关键点的方式连接为一体。

2.5.2考虑接触关系的几何模型

    建立了如图2.4B所示的几何模型，包括结构1、结构2和螺栓。建模时也取了以下两种简化方式对螺栓连接结构的边界进行处理：

    模型三：建立了较真实的螺栓模型，仅对螺纹部分进行了简化。将螺线形螺纹简化为直线形螺纹（如图2.5A）。建立模型三时，对螺纹和螺纹孔的处理是关键。由于螺纹结构形状较复杂，无法对螺纹部位的网格进行整体划分高级网格。因此，必须在分网之前将结构合理的分割为数个形状规则的子结构，利用“Sweep”功能对其进行体扫略划分。

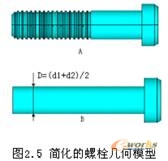
    模型四：不考虑螺纹结构，将其简化为圆柱体（如图2.5B）。螺栓与其它连接件的接触关系设置为“永远绑定”。    

     图2.5B中：  d1为螺纹牙顶圆直径 

    d2为螺纹牙底圆直径