1引言

    螺栓连接结构具有方便安装、拆卸等优点，在航天领域具有广泛的应用。螺栓连接的可靠性直接关系着连接件的整体结构完整性，决定整个系统能否正常工作。虽然螺栓连接件多为标准件，一般按国家标准选用后，其机械性能完全可以达到使用要求，但航天产品对可靠性要求极高，尤其是在生产与装配中的偏差会对其性能产生很大的影响。针对实际问题，通过结构有限元数值计算，研究不同工况条件下，螺栓连接结构的应力、变形情况，为产品的结构完整性提供理论参考。

    在进行螺栓连接结构的应力、变形情况数值分析时，通常考虑两个方面：一是考虑螺栓与其连接结构存在接触的边界条件下，分析整体结构受载后的应力、变形情况，可以根据螺栓的实际尺寸建立数学模型，用连续结构单元进行网络划分，不但可以使有限元模型准确，还可精确得到螺栓连接结构的应力、变形分布，但是模型较为复杂，计算自由度多，容易造成过长的计算机时；二是螺栓与其连接结构存在接触的边界条件下，分析整体结构受载后的应力、变形情况，通常对螺栓结构进行简化或采用耦合自由度的方法来描述螺栓的连接关系，可以大量节约计算机资源，提高计算效率，但是在自由度耦合处附近的应力、应变数值计算结果的准确性稍差一些。

    本文结合上述两个方面，以实际工程中设计出的螺栓连接结构为研究对象，应用ANSYS软件分别建立有限元模型采用数值模拟方法，研究探讨了螺栓连接结构在不同工况下边界处理方式对整体结构应力、变形的影响，给出了数值计算结果并对结果进行了分析，给出了相应的结论，为工程设计提供了理论参考，也为数值求解螺栓连接结构提供了可对比优选的数值建模方法。

2计算模型

2.1本构关系

    结构有限单元法中应力-应变D的本构关系一般可表达为：

    {σ}= [D]{ ε^el}   （1）

    其中：

    {σ} ：应力矢量；

    [D] ：刚度矩阵；

    { ε^el} ：应变矢量。

    弹性矩阵[D]的逆矩阵[D] ^-1可以表示为：

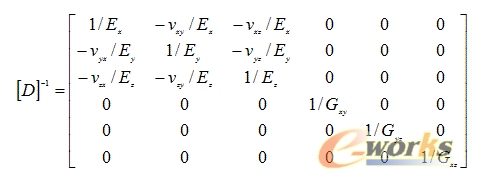
     其中：

      E_x：x方向的弹性模量；

      ν_xv：主泊松比；

      ν_vx：副泊松比；

      G_xv：xy平面的剪切模量。

2.2接触设置

    一般接触单元有线性接触单元和二次接触单元，下面以线性接触单元为对象，研究线性接触单元的各种不同接触情况下(法向接触和切向接触)，接触力的计算和切线刚度矩阵的计算过程。

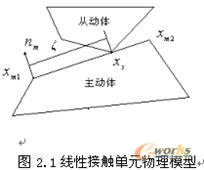
    在线性插值单元中，平面的边界可看作多边形。当多边形的一个尖点落在另一个物体中，则物体之间发生接触。取其中一个物体作为主体，另外一个作为从体。主体上的节点χ_m1、χ_m2以及从体上的穿透点χ₅构成一个接触单元。线段χ_m1χ_m2上的任意一点可由方程求得：

    χ_m(ζ)=χ_m1+(χ_m1-χ_m2) ζ         (0≤ζ≤1)        （2）

    接触模型的法向矢量、切向矢量和主从体之间的接触距离可以分别表示为：

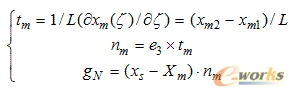
    接触问题属于典型的状态非线性问题，通常的数值解法是将之转化为优化问题求解，而接触是典型的含有不等式约束的优化，需要转化为不含不等式约束的问题，常用的数值方法就是拉格朗日法和罚函数法，归根到底是求解含有位移和接触间距的泛函的变分问题。本文中的螺纹啮合是一种典型的接触问题，在螺纹啮合的过程中，实际上就是一种螺齿之间不断相互接触传递力作用的过程。为了模拟螺纹啮合的特点，在建模过程中定义螺纹啮合接触面和目标面。有限元计算算法的选择是解决如何建立数学方程描述物理模型、几何运动规律及本构规律，并使系统处于平衡以及如何求解该方程的基础。罚函数法最为简单，它概念简单，应用方便。但是惩罚因子的取值非常关键，取值过小对结果影响也很小，过大则可能导致求解方程的病态。本文在计算接触力时，选用了拉格朗日乘子法方法，它克服了罚函数法过分依赖接触刚度的缺点，计算精度和计算效率都能保障。拉格朗日乘子法在解决接触问题时，虽然会产生一定量的“接触穿透”，但接触穿透通常都是一个非常小的数值，可以进行适当的调节，并不会影响数值计算精度。