1 引言
计算含有表面裂纹的平板以及构件的应力强度因子的方法有很多,如有限元法、边界元法、解析法、权函数法、切片合成法和线弹簧法等。应力强度因子手册中收编了许多种典型裂纹体模型应力强度因子的解。但对于结构或裂纹形状复杂和受复杂载荷作用的结构件,很多情况下应力强度因子的解难以从现有手册查到。有限元方法不受裂纹体几何及载荷形式的限制,因而,在断裂力学中得到广泛的应用,其中以Newman-Raju[1]和X.B.Lin、R.A.Smith[2]研究内容和结果具有代表性。
用有限元法研究裂纹体应力强度因子,目前最大的困难仍然是裂纹体有限元网格模型的建立。划分网格是建立有限元模型的一个重要环节,所划分的网格形式对计算精度和计算规模将产生直接影响。为建立正确、合理的有限元模型,本文对裂纹体网格的剖分做了研究,并利用ANSYS软件建立了含表面裂纹的平板模型。在该模型的基础上,通过对裂纹前缘奇异单元的边长L与裂纹深度a之比L/a、围绕奇异单元的单元层数R以及裂纹前缘每层单元划分的份数m(网格的疏密)的处理,详细讨论了有限元网格的划分对裂尖应力强度因子计算结果的影响。
2 计算模型
2.1裂纹几何形状的基本假设
(1) 裂纹相对结构对称面是对称的,分析时只需取构件的四分之一来计算;
(2) 裂纹的扩展方向沿裂纹线的法线方向;
(3) 裂纹面的形状呈半椭圆状,深度为a,长度为2c。
2.2 应力场强度因子的计算方法
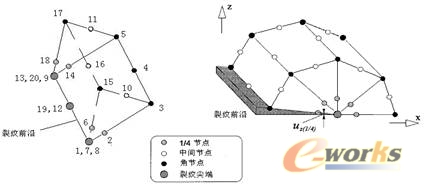
图2.1 裂纹尖端附近的网络构造
裂纹前缘的应力场存在一个数学上无限大的奇异点,一般多项式有限元很难模拟,除非在裂纹前缘附近用很小很密的单元。而且有时可能行不通,当计算机资源受到限制时效率很差。为了模拟裂纹前缘应力和位移的特性,70年代中期,亨舍尔(Henshell)、邵(Shaw,1975)和巴索姆(Barsoum,1977)各自独立地构造了一种裂纹前缘单元(也称奇异单元),提出了一个简便地反映缝端应力奇异性的方法,如图2.1所示。把1-7-8-12-19-20-13-9平面退化成一条直线1-19-13,并把2、6、14、18等4个边中点移至1/4边长处, 在角点附近即出现日r1/2级的应力奇异性,就得到三维退化奇异等参单元。
Barsoum证明了在裂纹表面1/4处的应力强度因子可用下列公式估计:
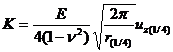
其中r(1/4)是相对裂纹前缘的1/4节点位移,如图2.1;E为弹性模量;v为泊松比。
2.3有限元模型生成
本文中裂纹前缘采用四分之一20节点等参退化奇异单元,用四分之一节点来代替裂纹尖端节点,以适应该处的应力奇异。为比较裂纹前缘的应力强度因子计算精度,研究了裂纹前缘奇异单元的边长L与裂纹深度a之比L/a和围绕奇异单元层数R以及裂纹前缘每层单元划分的份数m对计算结果的影响。有限元模型生成过程如下:
(1) 将模型分成两部分:裂纹体模型和非裂纹体模型,其中裂纹体模型通过体旋转生成椭圆部分,可以自动生成R为1到9围绕奇异单元层数,而非裂纹体模型单元划分得较大些,以减少计算工作量;
(2) 将裂纹前缘单元退化成由solid95蜕变而成的奇异单元,图2.1所示。
(3) L/a的选择问题,文献[3]建议L与裂纹深度a之间的比值(L/a)应该小于0.1,文献[4]建议该比值应该介于0.05和0.15之间,有限元分析软件ANSYS的技术文件则建议L/a小于1/8。本文将取L/a=0.02、0.04、0.06、0.08、0.1、0.12对该问题作进一步研究,以使L/a的确定更为明确。
(4) 关于围绕奇异单元的单元层数R,文献[3-7]都采用了2层以上的网格,本文将对该问题作进一步研究,取R=1到9层,以使围绕奇异单元层数的确定更为明确。如图2.2
(5)裂纹前缘每层单元划分的份数m(网格疏密),较多的有限元模型采用m=4,本文将对该问题作进一步研究,取m=4和8,以使m的确定更为明确。如图2.2