3. L/a、R和m对应力强度因子计算结果的影响
形状系数Y考虑了边界或其它裂纹离该裂纹远近程度的影响,裂纹的走向以及形状等因素的效应,对不同情况的应力强度因子的确定,归结为对Y的确定。而且Y是无因次的,应用方便,也便于与其它结果比较.其中
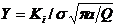
以含半椭圆表面裂纹的平板为例研究其在拉伸载荷形式下不同的L/a、R和m值对表面裂纹形状系数计算结果的影响,并与Newman-Raju公式[1]计算结果作对比。
当a/c=0.4、a/t=0.2时,同一拉伸载荷作用下计算结果对比
| 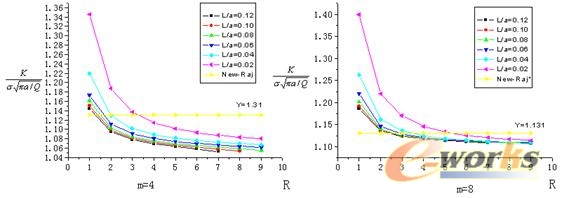 |
| 图3.1同一拉伸载荷作用下形状系数计算结果对比(a/c=0.4、a/t=0.2) |
当a/c=0.4、a/t=0.4时,同一拉伸载荷作用下计算结果对比
| 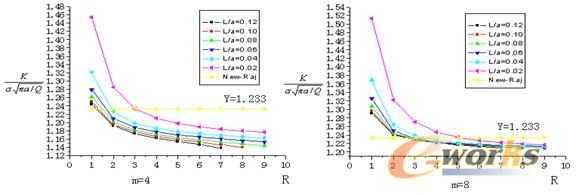 |
| 图3.2同一拉伸载荷作用下形状系数计算结果对比(a/c=0.4、a/t=0.4) |
当a/c=0.4、a/t=0.6时,同一拉伸载荷作用下计算结果对比
|  |
| 图3.3同一拉伸载荷作用下形状系数计算结果对比(a/c=0.4、a/t=0.6) |
从图3.1、3.2和3.3中可以看出在a/c=0.4保持不变、a/t逐渐增加的情况下,形状系数逐渐增大。比较L/a、R和m三个参数,其中L/a对形状系数的影响最为显著,而R在小于3时对形状系数的影响较为显著。
(1) 当m=4时
围绕奇异单元层数R的增加,使形状系数逐渐减小,并且随着L/a的减小有趋于一致的趋势,但当L/a=0.12时与其它L/a的结果相差较大。所以,为保证有限元模型的计算精度,L/a的取值应小于0.1。
当R<3时,由图3.1、3.2和3.3可以看出只有L/a(为0.02)较小时,计算结果才与Newman-Raju公式计算的结果比较接近;但是,当裂纹前缘单元尺度取得太小时,与之紧相邻的普通单元中的位移和面力仍将分别具有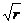 和
和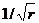 的渐进行为,而普通的中节点单元描述不了这种渐进行为。
的渐进行为,而普通的中节点单元描述不了这种渐进行为。
当R>2时,图3.1、3.2和3.3计算结果与Newman-Raju公式计算结果比较相对误差在0.5%~7.2%.,其中R=3(或=4)时,图3.1、3.2和3.3计算结果与Newman-Raju公式计算结果比较相对误差在0.5%~5%。
(2) 当m=8时
各参数之间与m=4有相同的变化趋势。但从图中可以看出,m=8的计算结果比m=4的结果更接近于Newman-Raju公式计算结果,当R>2时,图3.1、3.2和3.3计算结果与Newman-Raju公式计算结果比较相对误差在2.3 %以内。
按照本文的有限元模型生成方法,研究了L/a、R和m值对表面裂纹形状系数计算结果的影响。结果表明随着L/a的逐渐变小,形状系数计算结果逐渐增大。这意味着随着L/a的不断减小,一方面计算资源耗费加大,另一方面也导致求得的形状系数较真实值偏大。因此,从经济性、安全性和工程精度要求出发,同时参考其它文献和本文计算结果,本文作出如下建议:L/a值在0.04~0.08之间,R=3(或=4),m=8即可。
4 小结
本文描述了一种基于有限单元法计算表面裂纹应力强度因子的方法,建议了一种裂纹前缘网格形式,提供了一种通过体旋转能方便创造包含裂纹体三维网格的思路。
(1) 按照本文方法建立含裂纹平板结构有限元模型,其形状系数求解结果和公认的Newman-Raj u公式计算结果相对误差在工程精度范围内。这表明本文网格技术的正确性。
(2) 裂纹前缘奇异单元取得(如L/a=0.02时)太小时,计算误差将变得较大
(3) 虽然Newman-Raju公式计算方法能提供具有较好精度的表面裂纹应力强度因子的估算结果,但只能用于规则平板、中心裂纹的情况。使用本文提供的全三维有限元分析方法对平板表面裂纹的形状因子进行分析不但准确,而且使用可行,可以建立各类含表面裂纹的复杂结构模型。这就为用有限元分析表面裂纹应力强度因子在工程中的直接应用,提供了更大的方便。
[参考文献]
[1] Newman Jr. JC, Raju I.S. An empirical stress intensity factor equation for the surface crack. Engng Fracture Mech 1981;15:185-92.
[2] Lin XB, Smith RA. Finite element modelling of fatigue crack growth of surface cracked platesDPart I:The numerical technique. Engng Fracture Mech 1999;63:503-522 .
[3] J. J Cao, G. J. Yang, J. A. Paker, F. M. Burdekin. Crack modeling in FE analysi of circular tubular joints. Engineering Fracture Mechanics 1998,61:537-553
[4]Anthony R.Ingraffea,corneliu manu.stress-intensity factor computation in three dimensions with quarter-point elements. international journal for numerical methods in engineering. 1980, vol. 15, 1427-1445
[5] S. P. Chiew, S. T. Lie, C. K. Lee, Z. W. Huang. Stress intensity factors for a surface crack in a tubular T-joint[ J].International Journal of Pressure Vessels and Piping. 2001,78:677-685
[6] Bowness D, Lee MMK. Prediction of weld toe magnification factors for semi-elliptical cracks in T-butt joints. Int J Fatigue 2000;22:369-387.
[7] M. M. K. Lee, D. Bowness. Fatigue Analysis of Tubular Joints Using Finite Elements. Fatigue in Offshore Structures.1996,Vol.1,223-257