1 前言
电磁散射理论表明,雷达目标的电磁散射特性在频域可粗略的分为三个区域:瑞利区(目标尺寸远小于入射波长)、谐振区(二者处于同一数量级)、光学区(目标尺寸远大于入射波长)。对于目标瑞利区的雷达截面积的研究仅仅停留在对于规则几何体目标的研究,比如球体,圆柱体,旋转椭球体,锥体等等[1] [2]。对这些规则几何形状的目标(以下称为简单目标)经过研究可以精确的划分瑞利区,并可以给出严格的数学表达。目前国内关于该问题的分类和描述存在不完善的地方[3] [4];并且对于复杂目标的瑞利区,目前仍然没要好的通用划分方法。
目标散射区域划分是相对于入射波的波长来说的。相对于微波波段的波长来说一般复杂军事目标都处于光学区。而对于高频雷达(工作在短波段,2-30MHz)来说,大型飞机,水面舰船目标等均处于谐振区;而导弹和飞机目标则处于瑞利区;所以选取二者作为典型的复杂目标来研究。
本文通过采用ANSYS-CHINA公司提供的以矩量法和快速多极子为内核的FEKO软件计算得到简单目标圆柱体和圆锥体以及复杂目标导弹和飞机目标的RCS,分析目标RCS在瑞利区的变化。研究以往对于该区域简单目标的目标特性描述存在的问题。结合复杂目标的RCS变化,提出适用于简单目标和复杂目标的详细的分类方法并分别给出了对其RCS进行估计的方法和精确程度。
2 简单目标FEKO算例分析
2.1 定义和描述的缺点
目前,目标的瑞利区定义分两种:1)ka<1范围[3]。2)ka<0.5范围[2];k=2π/λ,为入射波波数,目标特征尺寸α定义为目标垂直于雷达视线截面中的最大尺寸的一半[2]。简单目标在瑞利区的RCS有以下经验公式给出[3]:
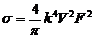 (1)
(1)
其中V表示目标的体积,F表示目标的形状系数,简单几何体的F可以通过查表获得,复杂目标的F未知,飞行器目标的F一般认为其值近似为1。公式(1)也仅仅是对目标RCS在对称轴轴向入射时候大致的估计。入射波在其他方向的入射时,目标RCS大都会在一定范围内缓慢的减小。
从理论上看上面关于雷达目标瑞利区划分和目标散射特性描述存在以下问题。首先,关于目标瑞利区的划分不统一,存在两种定义的范围。当然目标的瑞利区越大越好,因为相对于谐振区来说瑞利区的目标RCS的估计相对简单且准确。其次,当雷达视线相对于目标方位变化时,目标特征尺寸α变化,必然造成瑞利区范围划分不同,并且目标的RCS发生变化的范围也需要有一定的变化量的描述。以上是关于简单目标就存在这样一些问题。再次,关于复杂目标的瑞利区的划分以及RCS的估计没有较好的方法。
在实际的计算过程中,还会发现一些与以往理论不甚吻合的地方。根据公式(1)得出的结论,在瑞利区目标的RCS和频率的4 次方成正比,与实际计算结果之间也存在偏差,包括最简单的目标:球体,圆柱体,圆锥体等等。
以下就这些问题结合简单目标以及典型复杂目标的RCS的计算和分析,给出一些关于目标瑞利区划分以及RCS估计方面的方法和结论。
2.2 简单目标FEKO算例分析
为了说明前面指出的问题,采用FEKO软件计算了两个典型的体简单目标的RCS(基本尺寸见表1所示)。
表1 目标尺寸及高低瑞利区划分
| 模型 | 几何尺寸 | 瑞利区划分 |
| 圆柱体 | 柱高 5米 直径 1米 | 高区 13-19兆赫兹 低区 0-13兆赫兹 |
| 平底锥 | 顶角 20度 直径 1米 | 高区 24-36兆赫兹 低区 0-24兆赫兹 |
关于目标的瑞利区范围的问题,采用以往的理论,ka<1作为划分准则,根据表1中的目标的尺寸,平底锥的瑞利区在顶端入射时应为0-95兆赫兹左右;侧面垂直入射为0-37兆赫兹左右;从计算结果可以看出不同方向入射时目标的RCS曲线在30兆赫兹左右开始分离。如果以ka<0.5作为划分准则,则明显缩小了目标的瑞利区的范围。对于圆柱体目标的RCS的分析更加能够说明问题。以ka<1作为划分准则,根据表1中的目标的尺寸,圆柱体的瑞利区在顶端入射时应为0-95兆赫兹左右;侧面垂直入射为0-20兆赫兹左右;从计算结果可以看出,不同方向入射时目标的RCS曲线在15兆赫兹左右开始分离。但是顶端入射在大于15兆赫兹以后,进入了谐振区,这是和理论相矛盾的。如果以ka<0.5作为划分准则,也存在同样的问题。
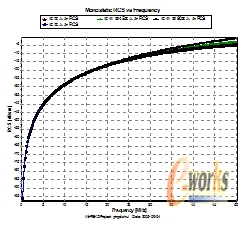
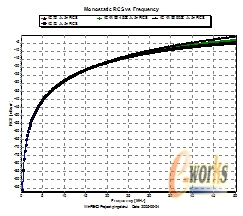
图1平底锥RCS曲线 图2 圆柱体RCS曲线
简单目标的RCS瑞利区的变化规律以公式(1)来描述,也是不够精确的,并且精确程度没有给出。可以通过比较和分析圆柱体和平底锥体,顶端入射情况下的RCS的FEKO软件计算值和(11)计算得出的理论值说明(比较结果如图3,4所示)。从图中可以看出二者的差距是很明显的,并且二者比较的范围仅仅是按照上面理论上定义的瑞利区的低端的一部分而已,随着频率的变大,二者的差距会变得更加剧烈。
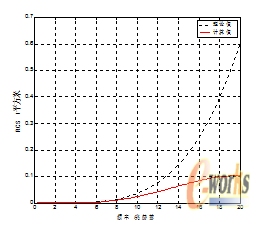
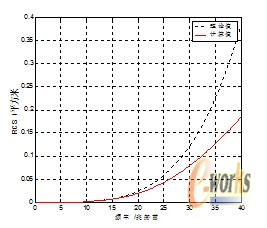
图3平底锥RCS比较曲线 图4 圆柱体RCS比较曲线
为了能够很好的解决这些问题,本文提出了新的目标瑞利区划分和RCS的估算方法目标瑞利区的划分以目标的最大的特征尺寸α为标准计算。划分为低瑞利区和高瑞利区:
(1) 低瑞利区范围为0≤ka≤2/3;目标RCS可以用(1)式准确的估计,误差小于1dB,基本不随雷达视线变化。
(2) 高瑞利区范围为2/3≤ka≤1; 目标RCS用(1)式估计的误差在5dB范围内。 随雷达视线方向改变也在5dB范围内。