3 复杂目标FEKO算例分析
为了研究复杂雷达目标在瑞利区的RCS变化情况,计算了某导弹在1-50兆赫兹频段内,不同雷达视线情况下的RCS,得到的变化曲线画在图7中(FEMAP网格化模型如图5示,基本几何尺寸别见表2)。雷达视线方向分别是迎头正方向,迎头斜45度、垂直弹体、弹尾斜45度、弹尾五个方向。由于雷达视线不同,目标的特征尺寸从3.1米缩小到1.3米,采用定义1所以对应的瑞利区范围分别约为0-15兆赫兹和0-37兆赫兹。显然和计算结果出入较大。采用定义2所对应的瑞利区范围分别约为0-7.5兆赫兹和0-18.5兆赫兹,符合瑞利区的特征,但是范围偏小。
表2 目标高低瑞利区划分
| 模型 | 粗略几何尺寸 | 瑞利区划分 |
| 导弹 | 弹长 6米 直径 0.5米 翼展 2.5米 | 高区 10-15兆赫兹 低区 0-10兆赫兹 |
| 飞机 | 长 17.米 宽 12.米 高 4米 | 高区 4-6兆赫兹 低区 0-4兆赫兹 |

图5 导弹目标网格模型 图6飞机目标网格模型

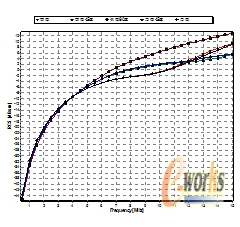
图7 导弹目标RCS曲线 图8 飞机目标RCS曲线
在该情况下,对于复杂飞行器雷达目标瑞利区同样存在高低区,适用前面提出的划分方法。按照以上划分标准对照目标的几何尺寸得出高低瑞利区范围列在表2中。对照上表以及计算结果图7,8,很直观的能够看出是符合的。显示了上面关于目标高低瑞利区划分对复杂目标来说也是正确的,并且对不同区域目标RCS近似变化规律描述也是恰当的。
复杂目标在瑞利区RCS的估计也可以通过形状同复杂目标的主体部分比较接近的简单目标来估算。选择三维尺寸和机身三维尺寸相同的椭圆柱或旋转椭球体作为近似目标。
以下就分别采用圆柱体近似估算导弹;椭圆柱体近似估算战机的RCS,并讨论在不同的瑞利区范围RCS估计的精度。
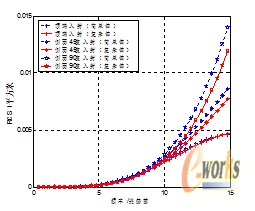
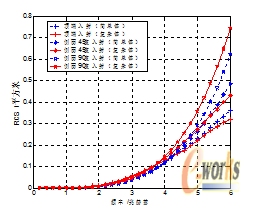
图9导弹目标RCS估计曲线 图10 飞机目标RCS估计曲线
通过计算结果图9,10可以看出无论是导弹还是战斗机这样的复杂目标,其瑞利区的RCS都可以采用形状大小相近的简单目标进行简化估算。而且估计的精度在低瑞利区可以保证在1dB左右;在高瑞利区可以保证在2dB范围内。
4 结论
采用FEKO软件计算无论是简单目标还是复杂目标的RCS具有较为理想的效果。通过FEKO计算结果的分析得到如下结论:
(1) 可将瑞利区分为高低瑞利区。在低瑞利区的目标的RCS基本不随雷达视线变化。因为在低瑞利区目标的尺寸相比于雷达波长来说较小,雷达视线变化对目标RCS影响很小;在高瑞利区的目标的RCS随雷达视线在一定范围内变化。
(2) 在不同的瑞利区区域内,简单目标RCS采用已有的经验公式计算,并给出了估计误差需要有定量描述。复杂目标则采用于其主体形状相似的简单目标的RCS作为近似估计。
该研究带有一定的经验性,虽然能够解决一些实际计算和估计的问题,但理论上作严格的推理还有待于作进一步的研究工作。
[参考文献]
[1] J.W.Crispin, A.L.Maffett. Radar cross section estimation for simple shaoes. Proceeding of The IEEE. 1965.8
[2] R.E.Kleinman. The rayleigh region. Proceeding of The IEEE. 1965.8.
[3] 盛新庆.计算电磁学要论. 北京:科学出版社. 2004,2.
[4] 黄培康,殷红成,许小剑. 雷达目标特性. 北京:电子工业出版社. 2005,3
[5] 阮颖铮等. 雷达截面与隐身技术. 北京:国防工业出版社. 1998,6.