考虑到Mie-Gruneisen状态方程不能描述弹丸速度高到一定值后，撞击所产生碎片云内材料的液化、气化等相变现象，因此在弹丸速度超过9km/s后，弹丸和防护屏材料Al 2A12使用Tillotson状态方程。该状态方程将（p,v）平面分为四个与冲击相关的区域，而不考虑Hugoniot曲线左侧只能通过绝热（非冲击）压缩达到的状态区域，如图4所示。Tillotson状态方程可对金属材料在超高速撞击现象中较大范围的压强和密度变化下的材料行为给出精确描述，它可以描述凝聚态和膨胀态(气化态)，覆盖固相、液相和气相，压力从常压到10¹⁴Pa。其初始参数有ρ₀以及系数a、b、A、B、α、β、e₀、e_s、e_s’^[10]。

    其中：e₀为初始比内能，e_s为升华能，e_s’是为保证区域II和区域IV的压力函数光滑连续而对e_s所做的修正；并且

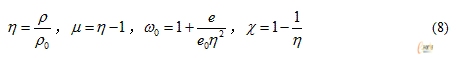
    对于Al 2A12，其Tillotson状态方程材料参数取值为^[8]：ρ₀ =2.785 g/cm³，A=7.5E7 kPa，B=6.5E7 kPa，a=0.5，b=1.63，a =5，β =5，e₀=5E6 J/kg，e_s =3E6 J/kg，e_s’ =1.5E7 J/kg。

    相应地，在弹丸速度超过9km/s后，弹丸和防护屏材料Al 2A12采用Steinberg-Guinan强度模型。该模型忽略了在高应变率下（10⁵/s以上）对强度影响较小的应变率效应，但考虑高温高压环境对材料的屈服应力Y和剪切模量G的影响，其表达式为^[11]：

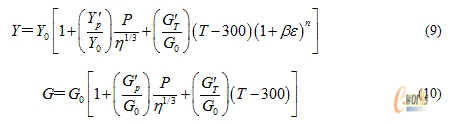
    限制条件为：

Y₀(1+βε)ⁿ≤Y_max   (11)

    其中：ε为等效塑性应变，T为温度，压缩比η=ρ/ρ₀，β、n为硬化功参数；G₀和Y₀分别为初始剪切模量和初始屈服应力，Y_max为最大屈服应力；Y_p’及G_p’ 、G_T’分别为屈服应力Y对压力P及剪切模量G对压力P和温度T的一阶偏导数，分别称为屈服应力的压力系数、剪切模量的压力系数和温度系数。对于Al 2A12，其Steinberg-Guinan强度模型材料参数取值为^[8]：G₀ =2.86E7 kPa，Y₀=2.6E5 kPa，Y_max=7.6E5 kPa，β=3.1E2，n =1.85E-1，G_p’ =1.8647，G_T’=-1.762E4 kPa，Y_p’=1.695E-2。

3、数值仿真结果与分析

3.1  数值分析方法

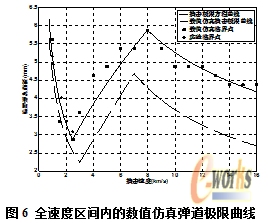
    对于每个撞击速度，改变弹丸直径以获得弹道极限。由于空间碎片与航天器的相对撞击速度区间为[1km/s 16km/s]，故撞击速度取为1-16km/s区间内的整数值，此外为与实验速度范围内的弹道极限结果进行有效对比，在3km/s速度以内增加计算点，即速度分别为1.5km/s和2.5km/s。在逼近临界弹丸直径时采用折半查找法，即取前一次穿孔和不穿孔的中间值作为下一次计算的初始值。最后在达到一定计算精度时（本文使用0.125mm），取使舱壁失效的最小弹丸直径与未使舱壁失效的最大弹丸直径的平均值作为该速度下的临界弹丸直径，并与相应的实验结果^[12]比较以验证数值仿真结果的准确性。

3.2  数值仿真结果与分析

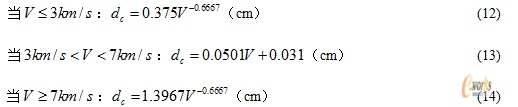
    按照上面所述的分析方法对计算结果进行分析，并采用最小二乘法对数值计算结果进行拟合，弹丸速度在3km/s以内的数值仿真结果、实验结果及由弹道极限方程得到的计算结果如图5所示。