日益增长的空间碎片严重威胁着航天器的安全在轨运行，造成航天器损伤及发生灾难性失效的事例已发生多起，有关防护微流星体和空间碎片超高速撞击的研究已得到了国内外的高度重视^[1]。由于空间碎片与航天器的相对撞击速度最高可达16km/s，其防护结构设计已成为航天器结构设计必须考虑的问题之一。1947年Whipple F.L.提出了铝合金双层板防护结构的概念，可有效抵御空间碎片及微流星体的超高速撞击^[2]。在大量超高速撞击实验的基础上，Christiansen E.L.在1993年提出了铝合金双层板Whipple防护的弹道极限经验方程^[3]，此后随超高速撞击数据库的进一步充实，又于2003年对其进行了修正^[4]。但由于国产航天材料与国外相比，在材料组分、生产工艺等方面都有一定区别，从而其材料性能也必然具有差异，这给经验方程的应用有效性带来了困难，必须进行细致的分析评价。本文对国内航天器常用的铝合金材料2A12和5A06构成的双层板防护结构进行了超高速撞击数值仿真研究，得到了特定条件下的弹道极限曲线和弹道极限方程，并与实验结果与最新的经验方程做出了对比分析。

1、结构及失效准则

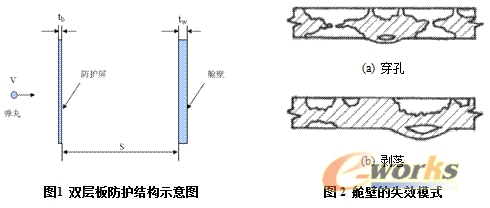
    所研究的双层板防护结构如图1所示。防护屏材料为铝合金2A12，厚度t_b为1mm；舱壁材料为铝合金5A06，厚度t_w为3mm；防护间距S为100mm。球形弹丸采用2A12铝合金，使用数值仿真并结合实验验证的方法研究双层板防护结构的正撞击弹道极限特性，即不同撞击速度下使舱壁失效的临界弹丸直径。采用的失效模式为舱壁出现穿孔或舱壁背面出现剥落^[5]，如图2所示。

2、数值建模分析

2.1  几何模型

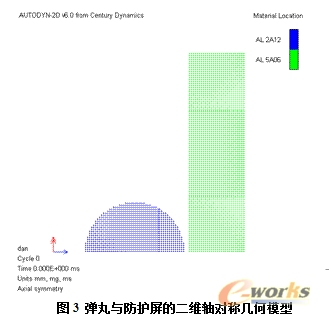
    光滑质点流体动力学法(Smoothed Particle Hydrodynamics，简称SPH)是一种无网格Lagrange算法，它通过将物体在空间离散成一组运动的光滑质点，并使用Lagrange插值法计算所有粒子从而得到整个物理问题的解。与传统基于网格的Lagrange、Euler或ALE等方法相比，SPH法可以更好地模拟超高速撞击薄板时碎片云的产生和发展，适合于模拟超高速碰撞这类高应变率、大变形的问题^[6]。因此，对本文的结构使用AUTODYN v6.0的SPH求解器进行计算。由于球形弹丸正撞击问题具有轴对称性，故建立二维轴对称模型，粒子的直径取为0.1mm，如图3所示。

2.2  材料模型

    采用Mie-Gruneisen状态方程，其方程如下^[7]：

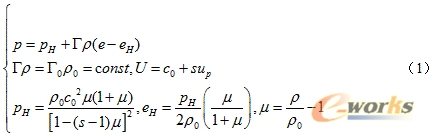
式中：p和e分别为静水压力和比内能；p_H和e_H分别为冲击Hugoniot曲线上静水压力和比内能的参考值；Γ和ρ分别为Gruneisen参数和密度，相应地Γ₀和ρ₀为初始Gruneisen参数和初始密度；U和u_p分别为冲击波波速和波后质点速度，c₀为体积声速，s为U和u_p之间线性关系的斜率；μ为压缩比。材料参数取值为^[8]：ρ₀ =2.785（2A12）、2.671（5A06）g/cm³，c₀=5328 m/s，S =1.338，Γ₀ =2.0。

    强度模型采用Johnson-Cook模型，其屈服应力σ_y与等效塑性应变ε_p、等效塑性应变率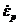和温度T之间的关系为^[9]：

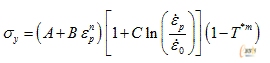   (2)

    式中：参考应变率ε₀＝1s^-1；A、B、n、C 和m是材料常数，A为材料在准静态下的屈服强度，B和n为应变硬化的影响，C为应变率敏感指数，m为温度软化系数。若室温为T_Room，熔点为T_Melt，则同系温度的定义为：

T^*=(T-T_Room)/(T_melt-T_room)   (3)

    材料参数取值为^[8]：A=2.65E5(2A12)、2.07E5(5A06) kPa，B=4.26E5 kPa，n=0.34，C=0.015，m=1.0，T_melt=775 K，T_room=300 K。

    由于实际的材料不能承受任意大的拉伸应力，因此需要定义失效模型来描述材料的极限强度。特别是在超高速撞击条件下，会有冲击波在弹丸和靶体中传播。它通过在自由表面的反射转变成足够强的拉伸应力波，从而使被作用材料产生剥落破坏。根据实验及分析比较，失效模型选取最大拉应力准则，其模型参数分别取为2.5E6(2A12)、2.2E6(5A06) kPa。