由图5可见,在实验速度范围内,数值仿真结果与实验结果及经验方程的结果都比较接近,三者相差不大,并且临界弹丸直径随速度的变化趋势是一致的,均随速度增加而临界弹丸直径减小。因此,可以认为数值仿真能够比较有效地获得其弹道极限数据与曲线,并且可以拓展速度范围,图6即为全速度区间内通过数值仿真方法得到的该铝合金双层板结构的弹道极限曲线,为对比分析还标出了实验得到的临界弹丸直径及弹道极限方程曲线。F
由图6可见,数值仿真与经验方程的弹道极限曲线均分成三个区域,曲线的趋势走向都是先下降再上升再下降。临界弹丸直径随速度变化有两个门槛值。对于第一门槛值速度,数值仿真结果为2.5km/s,经验方程结果为3.0km/s;对于第二门槛值速度,数值仿真结果为8km/s,而经验方程结果为7.0km/s。从这一点来看,两者比较吻合。在第一门槛值以内,两者差别较小。在速度超过第一门槛值后,数值仿真得到的弹道极限明显高于经验方程的结果,但两者的曲线形式很接近,相当于把弹道极限方程的曲线向上平移了一段距离。
对于本文的研究内容:1mm厚2A12铝合金防护屏,3mm厚5A06铝合金舱壁,间距10cm的防护结构,受2A12铝合金球形弹丸撞击,最终得到其弹道极限方程为:
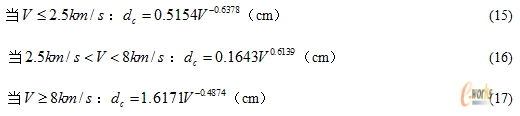
4、结论
(1) 数值仿真方法可有效获得铝合金双层板结构的弹道极限曲线,并可通过数据拟合得到特定双层板结构的弹道极限方程。
(2) 对于1mm厚2A12铝合金防护屏,3mm厚5A06铝合金舱壁,间距10cm的防护结构,受2A12铝合金球形弹丸撞击的条件下,现有的经验方程不能有效地预报其第二和第三速度区间内的弹道极限。因此,对于具体的防护结构,必须具体问题具体分析,采用数值仿真和实验验证相结合的办法确定其弹道极限曲线和弹道极限方程。
(3) 在通过了实验验证的前提下,本文得到了上述铝合金双层板结构受2A12铝合金球形弹丸正撞击下的弹道极限曲线和弹道极限方程,它可以为工程设计提供参考。
[参考文献]
[1] 闽桂荣,肖名鑫. 防止微流星击穿航天器舱壁的可靠性设计[J]. 中国空间科学技术, 1986,6:45-48
[2] Whipple F L. Meteorites and Space Travel[J]. Astronomical Journal, 1947, No.1161:131-147
[3] Christiansen E L. Design and Performance Equations for Advanced Meteoroid and Debris Shields[J]. International Journal of Impact Engineering, Vol.14, pp.145-156 ,1993
[4] Christiansen E L. Meteroid/Debris Shielding[R]. NASA TP-2003-210788, 2003:45-49
[5] Cour-Palais B G, Dahl K. Standardization of Impact Damage Classification and Measurements for Metallic Targets[R]. NASA Johnson Space Center, 1990:8-26
[6] Randles PW. Smoothed Particles Hydrodynamics: Some recent improvements and applications[J]. Computational Methods in Applied Mechanics and Engineering. 1996, 139(6):375-398
[7] AUTODYN Theory Manual, Revision 4.3[Z]. USA: Century Dynamics Incorporated, 2005
[8] Hayhurst C J, Livingstone I H. Advanced Numerical Simulations for Hypervelocity Impacts[R]. AUTODYN Simulations Final Report. ESTEC Contract No. 12469/97/NL/GD. 1998:1-20
[9] Johnson G R, Cook W H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures[A]. Proc. Seventh Int. Nat. Symposium on Ballistics, April 1983
[10] Tillotson J H . Metallic Equations of State for Hypervelocity Impact[A]. GA-3216, General Atomic, San Diego, CA, July 1962
[11] Steinberg D J, Cochran S G, Guinan, M W. Constitutive Model for Metals Applicable at High Strain Rate[J]. J. Appl. Phys. 1980, 51(3):215-232
[12] 管公顺,庞宝君,哈跃,张伟. 铝合金Whipple防护结构高速撞击实验研究[J]. 爆炸与冲击, 2005, 25(5):461-466