谐响应分析求解结构动力学方程：

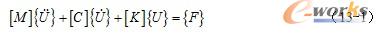
    式中，[M]为结构质量矩阵；[C]为结构阻尼矩阵；[K]为结构刚度矩阵；为节点加速度矢量；为节点速度矢量；{U}为节点位移矢量；{F}为力矢量。

    对于受迫振动的稳态响应，结构的所有节点均以相同的频率（激振频率）振动。由于存在阻尼，各节点的相位可以不同。因此，节点位移可表达为：

    式中，U_max为位移幅值；i为虚数，且i²=-1；ω为圆频率（单位为rad/s）；t为时间；φ为位移相角（单位为rad）；e^iφ和e^iωt为简谐振动的复数表达形式：

    将式（13-2）改写为：

    式中，{U₁=U_maxcosφ}，为位移实部；{U₂=U_maxsinφ}，为位移虚部。

    同理，力矢量也可表达为式（13-6）的形式：

    式中，{F₁=F_maxcosφ}，为力实部，F_max为力幅值，φ为力相角（单位为rad）；{F₂}={F_maxsinφ}，为力虚部。

    将式（13-5）和式（13-6）代入式（13-1），并消去e^iωt，得谐响应分析动力学方程：

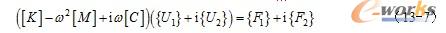
    ANSYS提供了3种方法求解式（13-7），即完全法、缩减法和模态叠加法，分别介绍如下：

    （1）完全法

    完全法是3种方法中最易使用的方法，它采用完整的系统矩阵计算谐响应（没有矩阵缩减）。完全法的优点是：

    1）容易使用，因为不必关心如何选取主自由度或振型。

    2）使用完整矩阵，因此不涉及质量矩阵的近似。

    3）允许有非对称矩阵，这种矩阵在声学或轴承问题中很典型。

    4）用单一处理过程计算出所有的位移和应力。

    5）允许定义所有类型的载荷：节点力、外加的（非零）位移和单元载荷（压力和温度）。

    6）允许在实体模型上定义载荷。

    7）可以包含预应力效应。

    （2）缩减法

    缩减法采用主自由度和缩减矩阵来压缩问题的规模。计算出主自由度处的位移之后，ANSYS可将解扩展到原有的完整自由度集上，这种方法的优点是：

    1）在采用稀疏矩阵求解器时比完全法更快且开销小。

    2）可以考虑预应力效应。

    缩减法的缺点是：

    1）初始解只计算主自由度的位移，要得到完整的位移、应力和力的解，则需执行扩展过程。

    2）不能施加单元载荷（如压力和温度等）。

    3）所有载荷必须施加在用户定义的主自由度上。

    （3）模态叠加法

    模态叠加法通过对模态分析得到的振型（特征向量）乘上因子并求和来计算结构的响应，它的优点是：

    1）对于许多问题，此方法比缩减法或完全法更快且开销小。

    2）模态分析中施加的载荷可以通过LVSCALE命令用于谐响应分析中。

    3）可以使解按结构的固有频率聚集，便可得到更平滑、更精确的响应曲线图。

    4）可以包含预应力效应。

    5）允许考虑振型阻尼（阻尼系数为频率的函数）。

    模态叠加法的缺点是不能施加非零位移。

    谐响应分析的3种方法均存在共同的局限性：

    1）所有载荷必须随时间按正弦规律变化。

    2）所有载荷必须有相同的频率。

    3）不允许有非线性特性。

    4）不计算瞬态效应。

    可以通过瞬态动力学分析来克服这些限制，此时应将简谐载荷表示为时间历程的载荷函数，详见第14章。