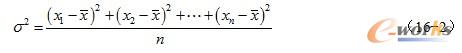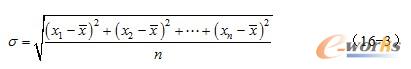对于随机过程，工程上常用的也是最基本的数字特征有均值（Mean）、方差（Variance）、标准偏差（Standard Deviation）、均方（Mean Square）和均方根（Root Mean Square，RMS）。

16.3.1  均值

    均值即平均值，也称为数学期望。设x₁，x₂，…，x_n为随机变量，则均值均值可表达为：

16.3.2  方差

    方差σ²表示对均值的偏离程度，定义为：

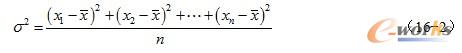
16.3.3  标准偏差

    标准偏差σ简称为标准差，为方差的算术平方根，即：

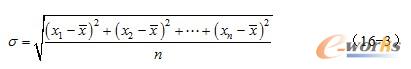
16.3.4  均方

    均方φ²定义为随机变量的平方的平均值，即：

16.3.5  均方根

    均方根φ为均方的算术平方根，即：

16.3.6  正态分布

    在ANSYS中，假定随机振动输入、输出的均值为零，且满足正态（高斯）分布（见图16-1）。则方差等于均方，标准偏差等于均方根。

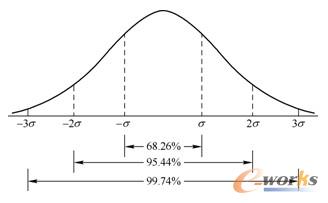
图16-1  正态分布的概率密度函数

    ANSYS默认输出1σ的解，表示响应值小于1倍标准偏差的概率为68.26%。由图16-1可知，响应值小于两倍标准偏差（2σ）的概率为95.44%，小于3倍标准偏差（3σ）的概率为99.74%。可见，尽管正态变量的取值范围是（-∞，∞），但它的值落在（-3σ，3σ）内几乎是肯定的事，这就是人们所说的“3σ”法则。