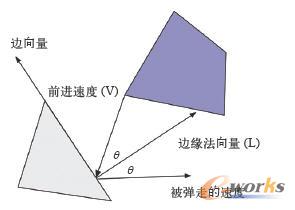
图1-23　通过向量来计算多边形在发生碰撞时被弹走的速度

    1.11.3.1　向量的大小

    虽说二维向量是对大小和方向这两个数值进行建模的，不过通常情况下，根据某个给定向量的x与y值来计算出这两个数值其中的一个，也是很有用的。你可以使用在学校数学课上学过的（或者，从《绿野仙踪》这部电影中看到的）毕达哥拉斯定理（Pythagorean theorem，又称勾股定理）来计算出某个向量的大小，如图1-24所示。

    毕达哥拉斯定理说：任何直角三角形的斜边，等于另外两边平方和的平方根。结合图1-24，就能更好地理解该定理了。与该定理相对应的JavaScript代码如下：

var vectorMagnitude =Math.sqrt(Math.pow(vector.x, 2) +

                                Math.pow(vector.y,2));

    上述JavaScript代码片段可以从一个名为vector的向量引用中计算出该向量的大小。

    讲完了如何计算某个向量的大小之后，我们来看看如何计算向量的另一个值：方向。

    1.11.3.2　单位向量

    向量运算经常会用到一个名叫“单位向量”（unit vector）的东西。单位向量是像图1-25所示的只用来指示方向的向量。

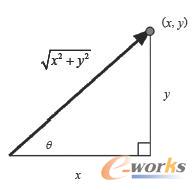
图1-24　计算向量的大小

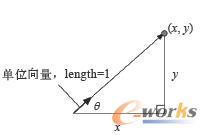
图1-25　单位向量

    之所以叫它单位向量，是因为其长度永远是“单位1”（1 unit）。如果要根据给定的向量来计算其单位向量，需要先把原来向量的大小去掉，只留下方向即可。在JavaScript代码中，可以这么来做：

    var vectorMagnitude =Math.sqrt(Math.pow(vector.x, 2) +

                                Math.pow(vector.y,2)),

    unitVector = new Vector();

    unitVector.x = vector.x / vectorMagnitude;

    unitVector.y = vector.y / vectorMagnitude;

    上述程序首先根据一个叫做vector的向量，沿用本小节前面讲过的办法，来计算出它的大小。然后，创建了一个新的vector对象，并将原有向量的x与y值分别除以原向量的大小，作为这个新单位向量的x与y值。

    读者已经学习了如何计算二维向量的两个分量，现在来看看如何对两个向量进行联合运算。