第一章 基础知识

    1.11.3.3　向量的加法与减法

    向量的加减法也是很有用的运算。举例来说，如果有两个力同时作用于某个物体，你可以把代表这两个力的向量相加，计算出这两个力的合力。同样，也可以从一个方位向量之中减去另一个，以求得两点之间的边界。

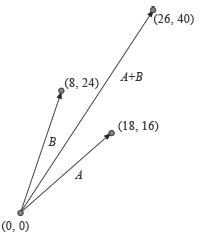
图1-26演示了如何根据两个给定的向量A、B，来进行向量加法运算。

    向量的加法运算很简单，像下面列出的程序清单这样，将向量的两个分量分别相加即可：

    var vectorSum = new Vector();

    vectorSum.x = vectorOne.x + vectorTwo.x;

    vectorSum.y = vectorOne.y + vectorTwo.y;

    向量的减法同样也很简单，像下面所列程序清单一样，将向量的两个分量分别相减即可：

    var vectorSubtraction = new Vector();

    vectorSubtraction.x = vectorOne.x -vectorTwo.x;

    vectorSubtraction.y = vectorOne.y -vectorTwo.y;

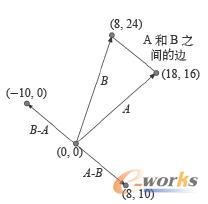
图27 两个向量的减法运算

    图1-27演示了将一个向量从另一个之中减去所得到的第三个向量，其方向恰好与两向量终点之间的边界方向是一致的。在图1-27之中，向量A-B与B-A互相平行，且两者都平行于向量A、B终点所构成的“边向量”。

    读者已经学会了如何进行向量的加减法，更为重要的是，了解到加减法所表示的几何意义，既然如此，我们再来看看向量的另一个数值：点积。

    1.11.3.4　两个向量的点积

    要计算两个向量的点积，需要将两个向量的对应分量相乘，然后再将乘积相加。下面这段代码可以计算出两个二维向量的点积：

    var dotProduct = vectorOne.x * vectorTwo.x +vectorOne.

    y * vectorTwo.y;

    计算两个向量之间的点积是很简单的，不过，这个点积的意义理解起来可就有些不太直观了。首先请注意，与两个向量的加减法运算结果不同，点积不是向量。专业人员把这种值叫做“标量”（scalar，也叫“纯量”），就是说，它仅仅是个数字而已。为了理解这个数字的意义，咱们研究一下图1-28。

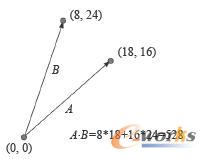
图1-28　两向量点积为正值的情况

    图1-28中所示的两个向量，其点积为528。该数值的重要性并不在于其大小，而在与其“大于0”这个事实。这意味着两个向量大概处在同一方向上。

    再来看看图1-29，该图中的两个向量，其点积为-528。因为该值小于0，所以我们可以推测出，这两个向量所指的方向大概不太一样。

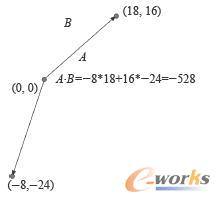
图1-29　两向量点积为负值的情况