第一章 基础知识

    判断两个矢量的终点是不是大致指向同一个方向，对于响应物体之间的碰撞来说，是一项很关键的技术。当某个运动的物体同某个静止的物体发生碰撞时，如果我们需要让运动的物体被静止物体弹开，那么就必须确保这个运动的物体在碰撞之后朝着远离静止物体的方向运动，而不是朝着静止物体的中心运动。通过计算两个向量的点积，我们可以精确地做到这一点，本书第8章将会讲解该问题。

    关于检测碰撞所用的向量知识，咱们就讲这么多，接下来，我们看看基础数学知识的最后一个小节：根据计量单位来推导等式。

    1.11.4　根据计量单位来推导等式

    读者在第5章中将会看到，动画的移动应该是以时间为基准的。因为一个物体的移动频率不应该随着动画的帧速率而改变。基于时间的运动（time-based motion）对于多人游戏来说尤为重要：你肯定不希望使用高配置电脑的玩家比别人移动地更快吧。

    为了实现基于时间的运动效果，本书中我们采用“每秒移动的像素数”（pixels per second）作为计量移动速度的单位。因此，为了计算动画当前帧所移动的像素数，我们需要知道两个信息：物体的移动速度是每秒多少个像素，以及当前动画的帧速率（frame rate）是每帧持续多少毫秒（milliseconds per frame）。我们所要计算的是：给定一个物体，求出它每帧所要移动的像素数（pixels per frame）。为了求得该值，我们得推导出一个等式来。等式的左端是每帧移动的像素数，右端则要包含每秒钟移动的像素数（也就是物体的速度）与每帧持续的毫秒数（也就是当前的帧速率），如等式1.4所示。

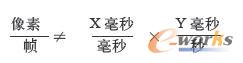
    等式1.4　推导基于时间的运动所用的计量单位，第1部分

    在上述“不等式（inequality）”之中，X表示以“每帧持续毫秒数”为计量单位的动画帧速率，而Y代表以“每秒移动的像素数”为计量单位的物体运动速度。正如该不等式所述，你不能简单地将“每帧持续毫秒数”与“每秒移动的像素数”相乘，因为如果那样做的话，将会得到“（毫秒×像素）/（帧数×秒）”这样没有意义的运算结果。那么，应该怎么算呢？

    回想一下1.11.1小节中讲述求解代数方程时所说的最后一条规则：你可以在等式的一端或两端同时乘以或除以1。已知1秒等于1000毫秒，所以“1秒/1000毫秒”等于1，根据该规则，我们可以给等式的右端乘以这个分数，于是得到了等式1.5。

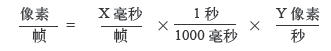
    等式1.5　推导基于时间的运动所用的计量单位，第2部分

    现在，我们可以来化简这个等式了。因为如果将两个分数相乘的话，那么其中一个分数分子中所含的计量单位就可以与另外一个分数分母中所含的相同单位互相消去。在本例中，我们按照等式1.6所述的方式进行化简。

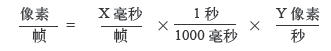
    等式1.6　推导基于时间的运动所用的计量单位，第3部分

    消去这些计量单位之后，我们得到了等式1.7。

    等式1.7　推导基于时间的运动所用的计量单位，第4部分

    将等式右端两个相乘的分数以简化形式写出来，就可以得到等式1.8。

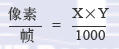
    X=用毫秒/帧表示的帧速率

    Y=用像素/秒表示的速度

    等式1.8　推导基于时间的运动所用的计量单位，第5部分

    当推导出一个等式时，应该向等式中带入一些简单的数值来检验一下，看它是否成立。在本例中，如果某个对象的移动速度是每秒100像素，且其帧速率是每500毫秒变换1帧，那么，不需要借助等式，即可看出，该物体在1/2秒内的移动距离是50个像素。

    将以上数字带入到等式1.8之中，就是500×100/1000，等于50，所以看起来我们所推导的这个等式的确可以根据移动速度与帧速率正确地计算出每帧移动的像素数。

    通常来说，如果要根据某些已知其计量单位的变量来推导换算等式的话，应该遵循如下步骤：

    （1）以一个不等式开始，将要推的结果放在左端，将其余变量放在右端。

    （2）根据等式两端的计量单位，给等式的右端乘以一个或多个分数。这些分数的值都要是1，它们所采取的计量单位要能够消去原来等式右端的计量单位，使其符合等式左端的单位。

    （3）将等式右端相同的计量单位消去。

    （4）将等式右端的各个分数相乘，合并为一个分数。

    （5）带入一些很容易被验证的简单数值进去，以确保推导好的等式能够算出期望的结果。