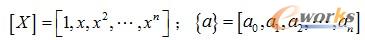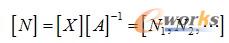插值就是构造一个在有限点能满足规定条件的连续函数。在有限元分析中，这些点是一个单元的节点，规定条件是一个场量的节点值（也可能是它的导数）。节点值很少是精确的，即使它们是足够精确的，插值法在其他位置给出的通常也会是近似值。在有限元分析中，插值函数几乎总是一个能自动提供单值连续场的多项式。

对于一维问题，根据广义自由度a_i、一个含有因变量φ和自变量x的插值多项式可以写成下列形式：

式中：

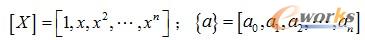
线性插值时n=1，二次插值时n=2，依次类推。a_i可以根据在已知的x值处φ的节点值来表示。节点值{φ_ε}和a_i之间的关系可以用符号表示为：

式中，[A]的每一行都是[X]在相应的节点位置的计算值。

由式（2-1）和式（2-2），可得：

式中：

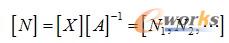
矩阵[N]中的每一个Ni被称为单元形函数。在有限元计算中，形函数矩阵把单元节点值同单元场函数联系起来。根据插值函数的阶数，可以把ANSYS中的结构单元分为低阶单元（单元采用一次插值）和高阶单元（单元采用二次或更高阶次插值）。对于二维和三维单元，将需要两个或3个空间自变量，但计算的原理和一维单元是一样的。