第二章 单元

2.2.1  概述

当用户使用命令或GUI方式生成连续单元时，ANSYS都要进行单元形状可行性检查。ANSYS先计算出单元的形状参数，如雅可比比率，然后与单元形状极限值比较。极限值可以通过SHPP、MODIFY等命令进行设置。如果超过极限值就会弹出警告信息或错误信息。

2.2.2  长宽比检查

除了电磁或流体单元外，所有单元都进行长宽比检查。表2-1给出了长宽比的极限值，该参数已经在多年前的有限元文献中出现过，并且是最容易理解的。

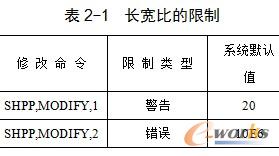
除非单元太长以至于数值四舍五入变成了一个因素（长宽比>1000），长宽比与分析的准确性没有多大的关联。有限元网格应该与所给问题的物理性质相适应，也就是在场梯度变化快的方向划分网格密一点，在场梯度变化慢的地方网格相应地划分粗一点。

有时要求单元的长宽比为10、100甚至1000，在某些情况下尝试人工限制长宽比有可能影响计算精度。

1．三角形单元长宽比的计算

三角形单元的长宽比用下列方式来计算，只使用单元顶点节点，如图2-1所示。

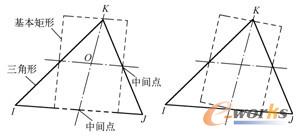
图2-1  三角形单元长宽比的计算

1）过三角形的一顶点作一条边的中线，然后再连接另两条边的中点，通常情况下这两条线是不垂直的。
2）以这两条线的交点为形心创建矩形，矩形的边通过三角形两条边的中点和一个顶点。
3）用上述方法可以创建通过另外两个顶点的矩形。
4）三角形的长宽比是这6个矩形中最长的矩形（即长宽比最大的矩形）的长宽比除以 。
三角形单元最理想的长宽比是1，即等边三角形。图2-2分别给出了长宽比为1和20的三角形。

图2-2  三角形单元的长宽比

2．四边形单元长宽比的计算

四边形单元的长宽比计算如图2-3所示，步骤如下：

1）如果单元的4个节点不在一个平面上，先计算出4个顶点的平均坐标和平均顶点法向，然后通过平均坐标点和平均顶点法向创建投影平面。以下的步骤都是在投影上进行。
2）连接四边形对边中点，交于单元中心。通常情况下，这两条线不相互垂直，也不垂直于四边形的各边。
3）通过各边中点创建矩形，所创建的矩形必须有两边垂直或平行于四边形的一条中线，较长矩形的长宽比即为四边形的长宽比。

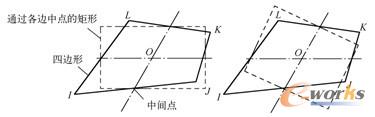
图2-3  四边形单元长宽比的计算

4）四边形最理想的长宽比是1，即正方形。图2-4分别给出了长宽比为1和20的矩形。

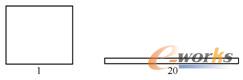
图2-4  四边形单元的长宽比

2.2.3  偏差角检查

ANSYS仅仅对SHELL28单元计算和测试剪切/扭转四边形的偏差角。表2-2给出了偏差角的极限值，这非常重要，因为单元来源于一个矩形。

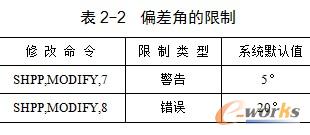
偏差角以每对相邻的边的夹角为基础，在二维空间用顶点的位置计算。最大的偏差是90°，是单元4个顶角中的一个。

图2-5所示给出了SHELL28单元的偏差角，其中最理想的偏差角为0°，此外也给出了偏差角为5°和20°的单元图。

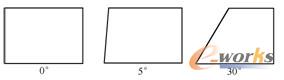
图2-5  SHELL28单元的偏差角

2.2.4  平行偏差检查

除了电磁或流体单元外，所有的四边形、有四边形面或截面的二维实体单元都要计算和检查平行偏差。表2-3给出了平行偏差的限制。计算表明，在线性应变过程中，当四边形对边变的不平行时，应力收敛速度变慢。

平行偏差的计算步骤如下。

1）忽略中间节点，在二维空间沿单元的各边画单位向量，将向量方向调整一致，如图2-6所示。
2）计算每对对边的单位向量的矢量积，通过余弦值求出两对单位向量的夹角值，较大的角度值即为平行偏差。如图2-6所示，两平行向量的矢量积是1，则 0°，两竖直向量的矢量积是0.342，则 70°。因此，这个单元的平行偏差为70°。

图2-6  平行偏差单元向量

3）最理想的平行偏差是0°，即平面矩形。图2-7所示为平行偏差分别为0°、70°、100°、150°和170°的四边形。

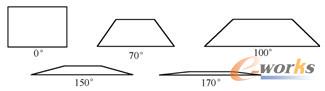
图2-7  四边形单元的平行偏差

2.2.5  最大顶角检查

除了电磁或流体单元外，所有的单元都要计算和测试最大顶角。表2-4给出了最大顶角的限制。有些有限元单元当顶角较大时（接近180°）会降低单元的性能，而小顶角不会。

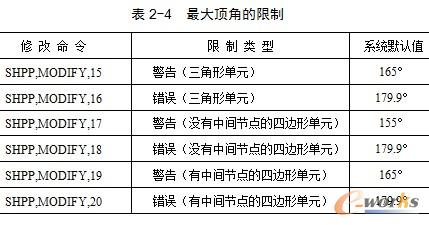
单元中各相邻边夹角中最大的角（如果有中间节点，中间节点将被忽略）。最理想的三角形单元最大顶角是60°，即等边三角形。图2-8所示为最大顶角为165°的三角形。最理想的四边形最大顶角是90°，即平面矩形。图2-9所示为最大顶角分别为90°、140°和180°的四边形。

图2-8  三角形的最大顶角

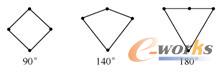
图2-9  四边形的最大顶角