第八章 代数方程和常微分方程求解

最简便方法是使用矩阵左除或是矩阵求逆的方法，求解线性方程组AX=b。
X= A\b
X=inv(A)*b
其中，A是方程组的系数矩阵，b是常数向量，X是解析解。
例8-3  求线性方程组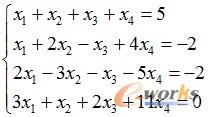的数值解。
% 线性方程组的数值解
AA=[1,1,1,1;1,2,-1,4;2,-3,-1,-5;3,1,2,11];             % 线性方程组系数矩阵
bb=[5;-2;-2;0];                                       % 线性方程组常数向量
disp('采用矩阵左除求出线性方程组的解：')
xx=AA\bb
disp('采用矩阵求逆求出线性方程组的解：')
zx=inv(AA)*bb
disp('计算残量：')
r=AA*zx-bb
disp('计算残量的模：')
R=norm(r)

M文件运行结果
采用矩阵左除求出线性方程组的解：
xx =
    1.0000
    2.0000
    3.0000
   -1.0000
采用矩阵求逆求出线性方程组的解：
zx =
    1.0000
    2.0000
    3.0000
   -1.0000
计算残量：
r =
  1.0e-014 *
    0.0888
    0.2220
   -0.4441
    0.1776
计算残量的模：
R =
  5.3475e-015
可见，采用矩阵左除或是矩阵求逆的两种方法的解是相同的，且计算精度是很高的。