第八章 代数方程和常微分方程求解

1．一维非线性方程
对于一维非线性方程f（x）=0求解，可以看做是单变量的极小化问题，通过不断缩小搜索区间来逼近一维问题的真解。因此，可以使用一维非线性方程优化解函数来求解。其调用格式是
[x,fx,flag]=fzero(fun,x0)
其中，输入参数中fun是非线性方程的函数表达式；x0是根的初值；输出参数中x是非线性方程的数值解；fx是数值解的函数值；返回参数flag>0时，表示求解成功，否则求解出现问题。
函数fzero所使用的算法为二分法、secant法和逆二次插值法的组合。

例8-4  求解一维非线性方程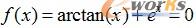的数值解。
% 求解单变量x非线性方程
x0=0.1;                                           % 解的初值
[xz,fz,flag]=fzero('atan(x)+exp(x)',x0);
disp('求解成功性判断参数：'), flag
disp('非线性方程的解：'),xz
disp('非线性方程解的函数值：'),fz

M文件运行结果：
求解成功性判断参数：
flag =
     1
非线性方程的解：
xz =
   -0.6066
非线性方程解的函数值：
fz =
 -1.1102e-016
可见，得到解的误差非常小，而且判断参数flag>0，表示求解成功。

2．多维非线性方程组
对于多维非线性方程组F（x）=0，其中f（x）=0是有多个非线性函数组成的向量函数

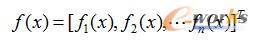
使用多维非线性方程组优化解函数求解的调用格式是
[x,fval,flag]=fsolve(fun,x0)
其中，输入参数中fun是非线性方程组的向量函数表达式；x0是根的初值；输出参数中x是非线性方程（组）的数值解；fval是数值解的函数值；返回参数flag>0时，表示求解成功，否则求解出现问题。
函数fsolve的作用是从根的初值x0开始，以逐渐减小误差的算法，搜索出满足多维非线性方程组fun的实根x和对应的函数值fval。

例8-5  求二维非线性方程组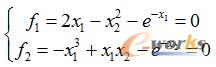的数值解。
x0=[2;3];                                        % 解的初值
% 定义非线性方程组表达式f和向量x
fun=inline('[2*x(1)-x(2)^2-exp(-x(1));-x(1)^3+x(1)*x(2)-exp(-x(2))]','x')
[xn,fval,flag]=fsolve(fun,x0);
disp('求解成功性判断参数：'), flag
if flag>0
    disp('方程组的解成功')
elseif flag<=0
    disp('方程组的解不成功')
end
disp('非线性方程组的解：'),xn
disp('非线性方程组解的函数值：'),fval

M文件运行结果：
求解成功性判断参数：
flag =
     1
方程组的解成功
非线性方程组的解：
xn =
    0.9978
    1.2755
非线性方程组解的函数值：
fval =
  1.0e-006 *
   -0.1945
   -0.3372
可见，两个非线性方程组解的函数值非常接近于0，说明其解的误差很小，而且判断参数flag>0，表示求解成功。