第一章 单片机基础知识

1.3  数制

    数制是人们对事物数量计数的一种统计规律。在日常生活中最常用的是十进制，但在计算机中，由于其电气元件最易实现的是两种稳定状态：器件的“开”与“关”；电平的“高”与“低”。因此，采用二进制数的“0”和“1”可以很方便地表示计算机内的数据运算与存储。在编程时，为了方便阅读和书写，人们还经常用十六进制数来表示二进制数。虽然一个数可以用不同计数制形式表示它的大小，但该数的量值是相等的。

1．进位计数制

    当进位计数制采用位置表示法时，同一数字在不同的数位所代表的数值是不同的。每一种进位计数应包含以下两个基本要素：
    （1）基数R（Radix）
    它代表计数制中所用到的数码个数。如二进制计数中用到的0和1两个数码；十进制计数中用到的0～9共10个数码。一般地，基数为R的计数制（简称R进制）中，包含0，1，…，R-1个数码，进位规律为“逢R进1”。
    （2）位权W（Weight）
    进位计数制中，某个数位的值是由这一位的数码值乘以处在这一位的固定常数决定的，通常把这一固定常数称为位权值，简称位权。各位的位权是以R为底的幂。如十进制数的基数R＝10，则个位、十位、百位上的位权分别为100，101和102。
一个R进制数N，可以用以下两种形式表示：
1）并列表示法，又称位置计数法：
(N)R＝(K n-1Kn-2…K1K0K-1K-2…K-m)R
2）多项式表示法，又称以权展开式：
(N)R＝Kn-1Rn-1+Kn-2 Rn-2+…+K1R1+K0R0+K-1R-1+…+K-mR-m
＝
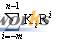
    上式中，m、n为正整数，n代表整数部分的位数；m代表小数部分的位数；Ki代表R进制中的某位数码，0≤Ki<R。
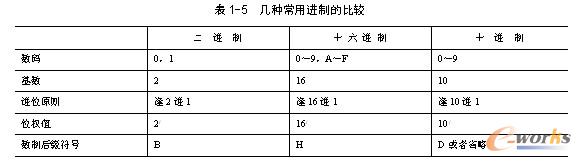
    表1-5给出了几种常用进制的比较。为避免混淆，除用（N）R的方法区分不同进制数外，还常用数字后加字母作为标注。其中，字母B（Binary）表示二进制数；字母D（Decimal）或不加字母表示十进制数；字母H（Hexadecimal）表示十六进制数。

 

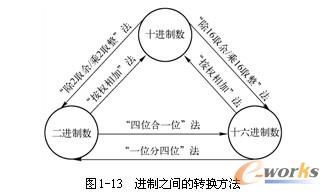
2．进制之间的转换

    进制之间的转换方法如图1-13所示，具体计算过程请参考“微机原理”教材有关内容。

    【例1-1】 （1）将二进制数11100011.100101B转换成十六进制数。
    （2）将十六进制数E3.94H转换成二进制数。
    （3）将二进制数1011.1010B转换成十进制数。
    （4）将十进制数53.375转换成二进制数。
    （5）将十六进制数DFC.8H转换成十进制数。
    （6）将十进制数208.625转换成十六进制数。
    解：（1）根据“四位合一位”法，(1110) (0011).(1001) (0100)B＝E3.94H
    （2）根据“一位分四位”法，E3.94H＝(1110) (0011).(1001) (0100)B＝11100011.100101B
    （3）1011.1010B＝1×23+0×22+1×21+1×20+1×2-1+0×2-2+1×2-3＝11.625
    （4）根据“除2取余”法和“乘2取整”法，53.375＝110101.011B
    （5）DFC.8H＝13×162+15×161+12×160+8×16-1＝3580.5
    （6）根据“除16取余”法和“乘16取整”法，208.625＝D0.AH

3．二进制编码

    由于计算机内的运算是二进制运算，因此，用0和1两个数字进行各种组合，将要处理的信息表示出来称为数字化编码。数字化编码分为数值型数据编码和非数值型数据编码，有正负、大小之分，能够进行算术运算的编码称为数值型数据编码；除数值型数据外的编码称为非数值型数据编码。将字符数码化后在计算机上表示成二进制数称为字符编码。字符编码属于非数值型数据编码。
    将数值型数据全面、完整地表示成一个机器数，应该考虑3个因素，即机器数的范围、机器数的符号和机器数中小数点的位置。
    （1）BCD（Binary Coded Decimal）码
    BCD码是用二进制数码按照不同规律编码来表示十进制数，这样的十进制数的二进制编码，既具有二进制的形式，又具有十进制的特点，便于传递处理。BCD码分为压缩的BCD码和非压缩的BCD码。压缩的BCD码是用一个字节表示2位BCD码；非压缩的BCD码是用一个字节的低四位表示一位BCD码，高四位没有意义，全为0。

分页    【例1-2】 求十进制数876的BCD码、二进制码和十六进制码。
    解：
    [876]BCD=1000 0111 0110 
    876=1101101100B=36CH 
    （2）ASCII（American Standard Code for Information Interchange）码
    ASCII码是美国信息交换标准代码的缩写，它采用7位二进制代码来对一个字符进行编码，可表示128个字符。ASCII码表见附录A。ASCII码字符种类如图1-14所示。

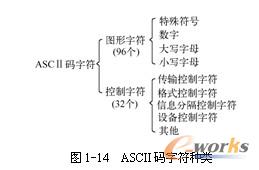
    通常将ASCII码的7位二进制代码分成两部分，高3位称为域（ZONE）代码；低4位称为数字（DIGIT）代码，见表1-6。域代码的意义见表1-7。

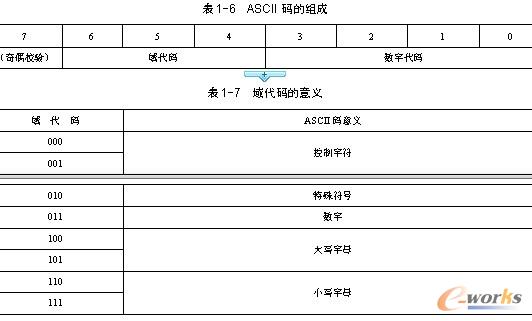
    ASCII码中的数字也可看成一种非压缩的BCD码，高四位为0011。