第一章 基础知识

    如果想用Canvas实现一些有趣的功能，那么必须得很好地了解一些基本的数学知识，尤其是代数方程、三角函数及向量运算。如果要编写类似电子游戏那样更为复杂的应用程序，那么还需要掌握如何根据给定的计量单位来推导等式。

    若是读者已经能够非常流畅地应对基本的代数运算与三角函数，并且能够根据给定的“每秒钟位移多少个像素”以及“每帧持续多少毫秒”来推导出“每帧的位移量”来，那么你略读一下本节就好了。不然的话，还是花些时间来研究一下这节的内容吧，它对于阅读本书的其余部分有很大帮助。

    我们先来讲讲代数方程的求解与三角函数，然后再来学习向量运算与如何根据计量单位推导等式。

    1.11.1　求解代数方程

    对于任意的代数方程，比如(10x+5)×2=110，都可以进行如下操作，使等式仍然成立：

    ·给等式两端同时加上任意一个实数。

    ·从等式两端同时减去任意一个实数。

    ·给等式两端同时乘以任意一个实数。

    ·让等式两端同时除以任意一个实数。

    ·给等式的一端或两端同时乘以或除以1。

    举例来说，(10x+5)×2=110这个方程式，可以这么来求解：先给等式两端同时除以2，得到10x+5=55，然后在等式两端同时减去5，得到10x=50，最后，让等式两端同时除以10，于是就求得x=5。

    上述规则中的最后一条看上去很奇怪。为什么要给等式的一端或两端同时乘以或除以1呢？在1.11.4小节之中，将会学习如何根据计量单位来推导等式，那时我们就会看到如何恰当地运用这条简单的规则。

    1.11.2　三角函数

    即便是最简单地使用Canvas，那也需要对三角函数有一个基本的了解才行。举例来说，本书下一章将会讲解如何绘制多边形，而这就需要你对正弦与余弦函数有一定的理解。我们先来简单地讲讲“角”的度量，然后再谈一下直角三角形。

    1.11.2.1　角的度量：角度与弧度

    Canvas中所有与角有关的API，都需要以弧度（radian）的方式来指定该角的值。JavaScript的Math.sin()、Math.cos()与Math.tan()函数也都采用弧度值。不过大部分人还是觉得角就是以角度（degree）来度量的，所以你得知道如何将角度转换为弧度。

    180度等于弧度。要想将角度转化为弧度，你可以先根据此关系建立像等式1.1这样的代数式：

    180度=弧度

    等式1.1角度与弧度的关系

    根据等式1.1可以推导出1角度等于多少个弧度，以及1弧度等于多少个角度。这两个推导等式分别记为等式1.2与等式1.3。

    1弧度=( π/ 180)×度

    等式1.2将角度化为弧度所用的等式

    1度=(180 /π)×弧度

    等式1.3将弧度化为角度所用的等式

    π约等于3.14，所以，45度等于(3.14/180)×45弧度，经过运算可以得知，等于0.7853弧度。

    1.11.2.2　正弦、余弦与正切函数

    为了有效地利用Canvas，你必须对正弦（sine，简称sin）、余弦（cosine，简称cos）及正切（tangent，简称tan）函数有一定的了解，所以说，如果你还不熟悉图1-21中所述的内容，那么现在必须把它记住才行。

    你也可以像图1-22中所画的这样，用圆周上某一点的X坐标与Y坐标来理解正弦及余弦函数。

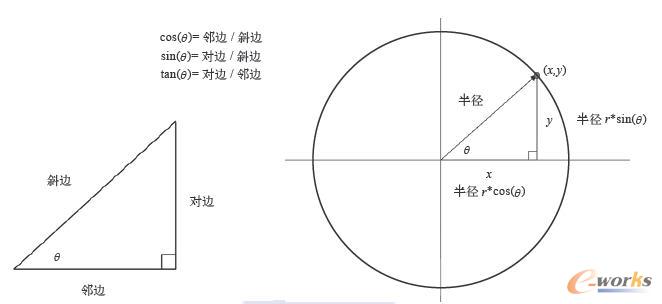
图1-21 正弦、余弦与正切函数的定义 图1-22 以半径、x坐标及y坐标来理解正弦及余弦函数

    给定某个圆的半径，以及一个从0度开始的逆时针角，我们就可以分别计算出圆周上某一点的x与y坐标了。其x坐标等于圆半径乘以该角的余弦值，y坐标等于圆半径乘以该角的正弦值。

    提示：用“Soak a toe, ah!”的口诀记住三角函数

    有很多种方式可以帮你回忆起如何从直角三角形中推导出正弦、余弦与正切函数的定义来。其中一个办法就是记住“SOHCAHTOA”这个口诀。SOH代表正弦（sine）、对边（opposite）及斜边（hypotenuse）；CAH表示余弦（cosine）、邻边（adjacent）及斜边（hypotenuse）；TOA代表正切（tangent）、对边（opposite）及邻边（adjacent）。

    1.11.3　向量运算

    本书中所用的二维向量（two-dimensional vector）都含有两个值：方向（direction）及大小（magnitude）。这两个值可以表达出各种各样的物理特性来，比如力（force）和运动（motion）。

    在本书第8章之中，将会频繁地用到向量，所以本小节我们先来讨论一下有关向量数学运算的基础知识。如果你对碰撞检测的实现不感兴趣的话，那么就可以放心地跳过这一小节了。

    在第8章的末尾，我们将会研究在两个多边形发生碰撞时，如何使其中一个多边形被另一个多边形弹开。该碰撞效果如图1-23所示。

    在图1-23之中，位于顶部的多边形正在向位于底部的多边形前进，这两个多边形即将发生碰撞。顶部那个多边形的碰撞之前的前进速度（incoming velocity）与碰撞之后被弹走的速度（outgoing velocity）都是以向量来建模的。在底部那个多边形中，即将与顶部多边形发生碰撞的那条边，也以向量来建模，我们称之为“边向量”（edge vector）。

    如果读者迫不及待地想要知道如何根据给定的前进速度与碰撞边界上的两个点，来计算出碰撞之后被弹走的速度，那么请跳至第8章阅读。然而，如果你还不太熟悉基本的向量运算，那么请在翻到第8章之前先把本小节的内容读完。