第二章 矩阵和数组及其运算
第五节 矩阵的乘法
矩阵乘(*)是指两个内维相同(前矩阵的列数与后矩阵行数相等)的矩阵进行乘法运算。
如果A是m×p阶矩阵,B是p×n阶矩阵,则矩阵A与B进行乘法运算得到的矩阵C=AB是一个m×n阶矩阵,其各个元素是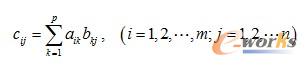
例2-4 有一个2行3列的矩阵A=[1,2,3;4,5,6]和一个3行4列的矩阵B=[7,8,9,10; 11,12,13,14;15,16,17,18],试对它们进行乘法运算。
A=[1,2,3;4,5,6]
B=[7,8,9,10;11,12,13,14;15,16,17,18]
运算结果:
C=A*B
A =
1 2 3
4 5 6
B =
7 8 9 10
11 12 13 14
15 16 17 18
C =
74 80 86 92
173 188 203 218
可见,矩阵A和B相乘得到的2行(矩阵A的行数)4列(矩阵B的列数)的矩阵C。
应当指出,矩阵乘法没有交换律。
说明:标量与矩阵相乘,是指标量与矩阵中的每个元素相乘,标量可以是乘数,也可以是被乘数。例如
>> A=[1,0,1;2,1,1;1,2,1]
A =
1 0 1
2 1 1
1 2 1
>> B=5*A
B =
5 0 5
10 5 5
5 10 5
如果A是m×p阶矩阵,B是p×n阶矩阵,则矩阵A与B进行乘法运算得到的矩阵C=AB是一个m×n阶矩阵,其各个元素是
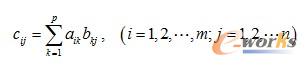
例2-4 有一个2行3列的矩阵A=[1,2,3;4,5,6]和一个3行4列的矩阵B=[7,8,9,10; 11,12,13,14;15,16,17,18],试对它们进行乘法运算。
A=[1,2,3;4,5,6]
B=[7,8,9,10;11,12,13,14;15,16,17,18]
运算结果:
C=A*B
A =
1 2 3
4 5 6
B =
7 8 9 10
11 12 13 14
15 16 17 18
C =
74 80 86 92
173 188 203 218
可见,矩阵A和B相乘得到的2行(矩阵A的行数)4列(矩阵B的列数)的矩阵C。
应当指出,矩阵乘法没有交换律。
说明:标量与矩阵相乘,是指标量与矩阵中的每个元素相乘,标量可以是乘数,也可以是被乘数。例如
>> A=[1,0,1;2,1,1;1,2,1]
A =
1 0 1
2 1 1
1 2 1
>> B=5*A
B =
5 0 5
10 5 5
5 10 5







