第二章 涡轮增压器压气机流场计算

    1.流体基本方程或控制方程

    涡轮增压器内部气体的流动是复杂的三维湍流流场，如果忽略工作过程中工作介质温度的变化以及温差造成的能量耗散，其流动受到质量守恒方程、动量守恒方程、能量守恒方程、组分守恒方程和体积力的约束或控制。

    在采用CFX求解器进行流场数值仿真计算时，需要求解流动基本方程。CFX使用全隐式多重网格耦合求解技术，这种求解避免了传统算法需要“假设压力项—求解—修正压力项”的反复迭代过程，却能同时求解动量方程和连续性方程。

    质量守恒方程常称作连续性方程，它所描述的物理意义为：单位时间内流体微元控制体中质量的增加，等于同一时间间隔内流人的质量减去流出的质量，其方程如下：

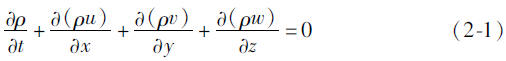
    或表示为

    若介质为不可压流体，密度p为常数，则方程(2-2)简化为：

    动量守恒方程即为著名的Navier-Stokes方程，简称N-S方程，其物理意义为：微元控制体中流体的动量对时间的变化率等于外界作用在该微元控制体上的各种力之和。笛卡儿坐标系下Navier-Stokes方程可表达为：

    其中，下标，代表无粘性，下标V代表粘性。式(2-4)中各参数表示如下：

    式(2-4)两端积分后可以写成：

    其中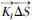，和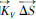分别代表无粘性和有粘通量(Flux Vector)。

    能量守恒方程的物理意义为：流入热量减去输出功等于内部能量变化率加上流出的焓减去流入的焓，其数学表达式为：

    其中：

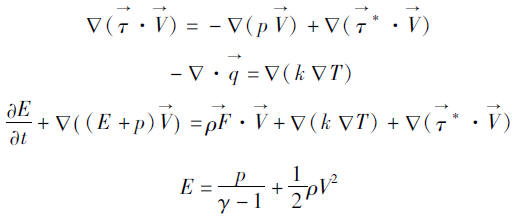
    质量守恒定律、动量守恒定律和能量守恒定律反映流体运动规律的三组方程的理论解只有在一些简单情况、简单边界条件下才能获得，在大多数情况下只能借助有限元、有限体或有限插分原理才能求得数值解。

    很明显，方程(2-4)和(2-5)这两个N-S方程是非线性的对流扩散型偏微分方程。一般情况下的N-S方程初边值问题解的存在性和唯一性尚未完全得到证明。只有在很苛刻的条件下，N-S方程解的存在和唯一性才能证明，例如，当质量力有势时。数学上已经证明N-S方程的解具有如下性质：

    1)定常的N-S方程的边值问题至少有一个解，但是只有当雷诺数较小时解才是稳定的。

    2)非定常平面或轴对称流动的初边值问题在一切时刻都有唯一解。

    3)一般三维非定常流动的初边值问题，只有当雷诺数很小时才在任意时刻都有唯一解。

    4)任意雷诺数的三维非定常流动的初边值问题，只有在某一时间区间内解是唯一的，时间区间的大小依赖于雷诺数和流动的边界，雷诺数越大则存在唯一解的区间越小。

    N-S方程初边值问题解的存在说明，在雷诺数较小时，存在唯一的确定性解，也就是定常或非定常层流解；当不满足解的唯一性条件时，N-S方程可能存在分岔解。一般认为，随着流动雷诺数的增加，流动由层流向湍流过渡的现象是N-S方程初边值问题解的性质在变化所致，层流是小雷诺数下N-S方程的唯一解；随着雷诺数的增加，出现过渡流动，这是N-S方程的分岔解；高雷诺数的湍流则是N-S方程的渐近不规则解。总之，无论是层流还是湍流都服从N-S方程。