第二章 涡轮增压器压气机流场计算

    2.湍流模型及数值模拟方法

    湍流是一种高度非线性的多尺度不规则流动。从表2-1看出，对于三维且较大的压力梯度以及中等的曲率和分离流动情况下流动模拟计算，应当采用低雷诺数下的湍流模型。表2-2中所示，低雷诺数模型解的边界层内层，y+的适用范围为1～10；高雷诺数模型解的对数边界层，y+的适用范围为20～50，但对数函数不适用于分离流。所以低雷诺数模型更有价值。

表2-1 适应不同类型流态的湍流模型

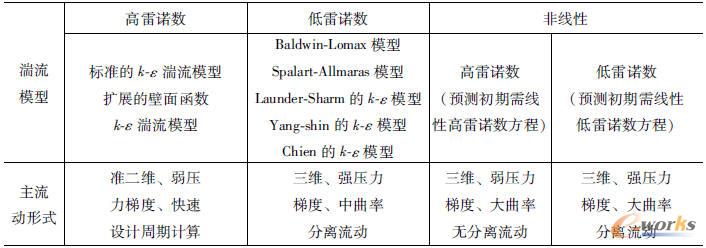
表2-2 不同湍流模型的y+

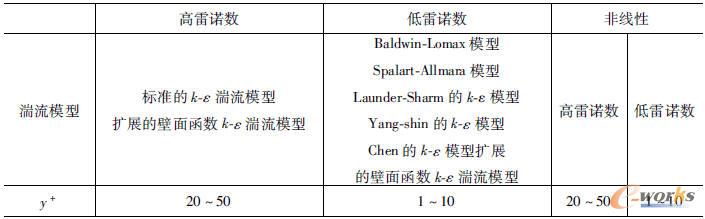
    对于压气机来说，其内部流动主要是湍流运动。根据表2-1、表2-2和图2-5，目前在叶轮机械粘性流动计算中最常用的湍流模型就是一方程的S-A模型和两方程的k-ε模型。

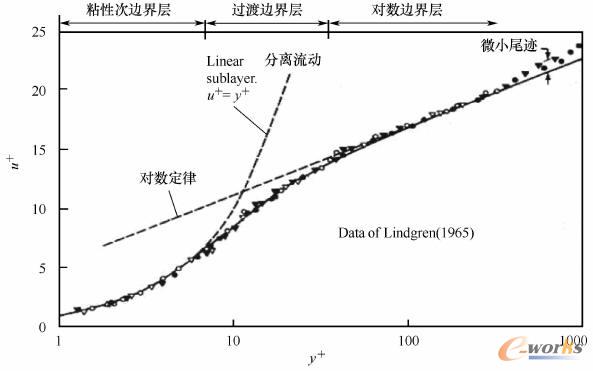
图2-5 边界层分布

    代数湍流模型通过混合长度来确定湍流粘性系数，与湍流动能无关。在湍流输运模型中，湍流粘性系数与湍流动能以及其他一些湍流量相关。对于可压缩流体的稳态流动，不考虑重力的影响，标准k-ε两方程模型的输运方程为：

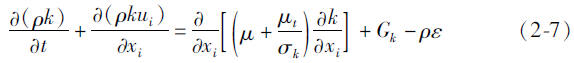
    和

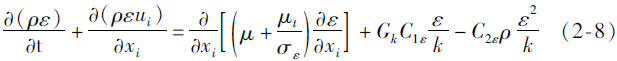
    式中 Gk-湍流生成项，表示平均速度梯度而产生的湍动能，Gk=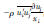

    μt——模型常量，μt=ρCμk2/εCμ、C1g。、C2ε、σk、σε。取值见表2-3。

表2-3 标准k-ε湍流模型常数

    从20世纪70年代以来，随着计算机技术的迅速发展，数值模拟已成为研究湍流的有效手段。根据计算条件和研究湍流的不同目的，各种湍流数值模拟方法的精细程度有不同的层次。湍流的数值模拟方法可以分为两大类：直接模拟方法和非直接模拟方法，如图2-6所示。

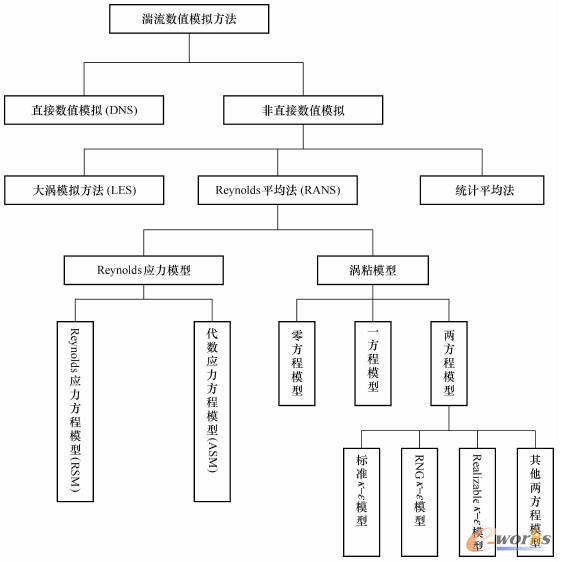
图2-6 主要湍流数值模拟方法

    研究湍流最精确的方法是直接数值模拟(Direct Numerical Simulation，简写为DNS)，即无须采用任何湍流模型直接求解三维瞬态N-S方程，就可得到各种不同尺度瞬时湍流流场。但DNS对内存空间及计算速度要求非常高，所以目前无法应用于真正意义的工程计算。

    雷诺平均（Reynolds Averaged Navier-Stokes，简写为RANS）就是把Navier-Stokes方程中的瞬时变量分解成平均量和脉动量两部分。对于速度，有：u_i=+u＇_i，其中，和u＇_i分别是平均速度和脉动速度；指标i的取值范围为(1，2，3)。

    类似地，对于压力等其他标量，也有：

    式中φ——标量，如压力、能量、组分浓度等。

    把上面的表达式代入瞬时的质量连续与动量方程，并取平均（去掉平均速度ui上的横线），可以把质量连续与动量方程分别写成如下的笛卡儿坐标系下的张量形式：

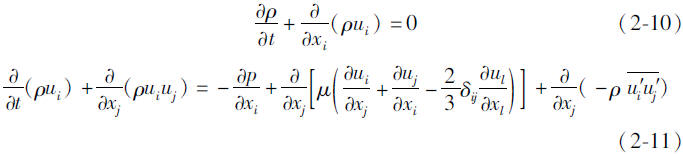
    式中p——密度；

    x——实际流动区域的空间坐标；

    指标i和j的取值范围为(1，2，3)。

    上面两个方程称为雷诺平均的Navier-Stokes(RANS)方程。它们和瞬时Navier-Stokes方程有相同的形式，只是速度或其他求解变量变成了时间平均量。额外多出来的项-ρ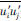是雷诺应力，表示湍流的影响。

    大涡模拟（Large Eddy Simulation，简写为LES）方法是介于直接数值模拟和Reynolds平均法(RANS)之间的一种湍流数值模拟方法。它的基本思想可以概括为：用瞬时的Navier-Stokes方程直接模拟湍流中的大尺度涡，不直接模拟小尺度涡，而小涡对大涡的影响通过近似模型考虑。总体而言，LES方法对计算机内存和CPU速度要求仍然比较高。