第二章 第2章 涡轮增压器压气机流场计算

2. 6. 1全叶片流道及网格的重新划分
   
      由于采用的是非定常设置，所以叶片的边界条件不能使用周期性边界条件，必须建立全叶片流道的模型，全叶片通道模型如图2-22所示。

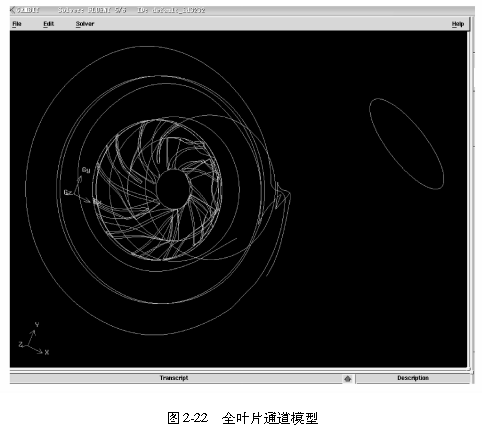
      与前面章节平均划分网格不同的是，为适应涡轮增压器内部结构的复杂性，采用多块网格生成方法生成高质量网格。考虑到不同流动区域的不同重要性，对旋转叶轮内部、蜗舌壁面附近的网格节点进行了加密控制和非等距处理。其中，进气部分网格节点数为4460个，旋转叶轮部分网格节点数为128000个，蜗壳部分网格节点数为149000个，网格节点总数共计281460个。叶轮进口和旋转扩压器出口2个动静元件交接的界面上，采用了滑移网格方法处理。

2. 6. 2选择解的算法

      FLUENT软件可以提供三种不同的算法:分离算法、隐式藕合算法、显式藕合算法。这三种算法都可以在很大流动范围内提供准确的结果，但是它们也各有优缺点。分离算法和藕合算法的区别在于:连续性方程、动量方程、能量方程以及组分方程的解的步骤不同，分离算法是按顺序解，藕合算法是同时解。两种算法都是最后解附加的标量方程。隐式算法和显式算法的区别在于线化藕合方程的方式不同。
   
      下面对这几种算法做一介绍。
    
      1、分离算法
      使用该方法，控制方程是顺序解出的，因为控制方程是非线性的，所以在得到收敛解之前，必须进行迭代。其过程包括:
      1)解的基础上，更新流体属性(如果计算刚刚开始，流体的属性用初始解来更新)。
      2)为了更新流场，动量方程用当前压力和表面质量流氢经安}}匝序解出。
      3)因为第一步得到的速度可能在局部不满足连续性方程，所以从连续性方程和线化动量方程推导出压力校正的泊松方程。然后解出压力校正方程获取压力和速度场以及表面质量流量的必要校正从而满足连续性方程。
      4)在适当时，用前面更新的其他变量的数值解出湍流、能量、组分以及辐射等标量。
      5)当包含相间来禺合日寸，可以用离散相轨迹计算来更新连续相的原页。
      6)检查设定的方程的收敛性。
   
      2、藕合算法
      该方法同时解连续性、动量、能量以及组分输运的控制方程。因为控制方程是非线性的和藕合的，所以在获取收敛解之前需要进行适当的解循环的迭代。其过程如下:
      1)在当前解的基础上更新流体属性(如果刚刚开始计算则用初始解来更新)。
      2)同时解连续性、动量、能量和组分输运方程。
      3)在适当的地方，用前面更新的其他变量的数值解出如湍流和辐射等标量。
      4)当包含相间来禺合日寸，可以用离散相轨迹计算来更新连续相的原页。
      5)检查设定的方程的收敛性。
   
      直到满足收敛判据才会结束上述步骤。
   
      3、隐式和显式线化算法
      在分离和藕合算法中，非线性控制方程被离散、线化为每一个计算单元中相关变量的方程组，然后用线化方程组的解来更新流场。
   
      控制方程的线化形式可能包括关于相关变量的隐式或显式形式。隐式算法原理为:对于给定变量，单元内的未知值用邻近单元的已知和未知值计算得出。因此，每一个未知值会在不止一个方程中出现，这些方程必须同时解来给出未知量。显示算法原理为:对于给定变量，每一个单元内的未知量用只包含已知量的关系式计算得到。因此未知量只在一个方程中出现，而且每一个单元内的未知量的方程只需解一次就可以给出未知量的值。
   
      涡轮增压器压气机内为高速可压流动，求解时网格要比较密。由以上方程算法分析，采用分离隐式算法比较合理，并通过计算得到每个时间步的压力和速度数据。

2. 6. 3控制方程及湍流模型
   
      压气机非定常流场计算所用的控制方程组及湍流模型与前面定常流场计算相同，控制方程采用三维雷诺守恒型N-S方程，湍流模型采用RN G k-ε模型，并取标准壁面函数。

2. 6. 4边界条件与初始条件
   
      给出空间离散和求解算法后，方程的求解还需要给定适当的初始条件和边界条件，它的合理与否也会影响计算收敛情况以及计算精确程度。
   
      1、迭代的初始条件
      迭代的初始条件是控制方程进行时间推进求解的初始参考状态，数值计算实验表明:初始场的选择一般并不影响最终所要得到的数值结果，但对达到收敛所需要的时间有很大影响，而且如果初始条件选择不当，会导致计算结果不收敛。因此，为了提高计算效率，选择高质量的初始条件是非常必要的。
   
      2、边界条件
      边界条件包括流动变量和热变量在边界处的值，它是FLUENT软件分析关键的一部分。在FLUENT中，有针对各种不同实际情况的进出口边界条件形式，它们可以自由组合，以形成合理的数值计算边界条件。边界条件分为:进出口边界条件，包括压力、速度、质量进口、进风口、进气扇、压力出口、压力远场边界条件、质量出口、通风口、排气扇;壁面边界条件，包括壁面、对称、周期等;内部单元区域边界条件，包括流体、固体;内部表面边界条件，包括风扇、散热器、多孔跳跃、壁面、内部等。
   
      其中经常用到的边界条件有:
      (1)压力人口边界条件压力人口边界条件用于定义流动人口的压力以及其他标量属性。它既适用于可压流，也可以用于不可压流。压力人口边界条件可用于压力已知但是流动速度和/或速率未知的情况。这一情况可用于很多实际问题，比如浮力驱动的流动。压力人口边界条件也可用来定义外部或无约束流的自由边界。
 
      (2)速度人口边界条件给定人口边界上的速度以及其他相关标量值。该边界条件适用于不可压缩流动问题，对可压缩问题不合适，否则该人口边界条件会使人口处的总温度或总压力有一定的波动。
   
      (3)质量人口边界条件该边界条件用于规定人口的质量流量。为了实现规定的质量流量中需要的速度，就要调节当地人口总压力。这和压力人口边界条件是不同的，在压力人口边界条件中，规定的是流人驻点的属性，质量流量的变化依赖于内部解。当匹配规定的质量和能量流速而不是匹配流人的总压时，通常就会使用质量人口边界条件。
   
      (4)压力出口边界条件压力出口边界条件需要在出口边界处指定静压。静压值的指定只用于亚声速流动。如果当地流动变为超声速，就不再使用指定压力了，此时压力要从内部流动中推断。所有其他的流动属性都从内部推出。
   
      在解算过程中，如果压力出口边界处的流动是反向的，回流条件也需要指定。如果对于回流问题指定了比较符合实际的值，收敛性困难就会被减到最小。
   
      (5)质量出口边界条件当流动出口的速度和压力在解决流动问题之前是未知时，FLUENT软件会使用质量出口边界条件来模拟流动。不需要定义流动出口边界的任何条件，FLUENT软件会从内部推导所需要的信息。
   
       (6)壁面边界条件壁面边界条件用于限制流体和固体区域。在粘性流动中，壁面处默认为非滑移边界条件，但是也可以根据壁面边界区域的平动或者转动来指定切向速度分量，或者通过指定剪切来模拟滑移壁面，也可以在FLUENT软件中用对称边界类型来模拟滑移壁面，但是使用对称边界就需要在所有的方程中应用对称条件。
   
      (7)周期性边界条件周期性边界条件用来解决物理模型，流动和换热具有周期性重复的特点。FLUENT提供了两种类型的周期性边界条件。第一种类型不允许通过周期性平面具有压降，第二种类型允许通过平移周期性边界具有压降，它能够模拟完全发展的周期性流动。
   
      本节压气机非定常计算以定常稳定状态为初始场，人口处质量流量为0. 087 ㎏/s，出口边界条件静压为标准大气压，壁面采用无滑移条件。当解呈现周期性变化即认为达到稳态。

2. 6. 5求解器的使用
   
      确定了模型和求解器后，运行求解器的一般流场为：
      1)选择离散格式。
      2)选择压力速度藕合方法(只用于分离求解器)。
      3)设定松弛因子。
      4)打开FAS多重网格(只用于藕合显式求解器)。
      5)对求解器设定作任何附加的修改。
      6)初始化解。
      7)激活适当的解监视器。
      8)开始计算。
    
    1、选择离散格式
      FLUENT可以选择每一个控制方程的对流项的离散格式(对于粘性项自动使用二阶精度)。当使用分离求解器时，在默认的情况下，所有的方程都是使用一阶迎风离散来解对流问题;当使用藕合求解器时，在默认的情况下，流动方程是二阶格式解出的，其他方程是用一阶格式解出的。
   
      一阶离散一般会比二阶离散收敛得好，但是精度要差，尤其是对于三角形或者四面体网格精度更差。如果使用二阶格式遇到收敛性问题，应该尝试使用一阶格式。
   
      2、选择压力速度藕合方法
      在分离求解器中，FLUENT提供了压力速度藕合的三种算法:SIMPLE , SIMPLEC以及PISO。定常状态计算一般使用SIMPLE或者SIMPLEC方法，对于过渡计算推荐使用PISO方法。PISO方法还可以用于高度倾斜网格的定常状态计算和过渡计算。需要注意的是，压力速度藕合只用于分离求解器，对于藕合求解器不可以使用。
   
      3、设定松弛因子
      由于流体力学中要求解非线性方程，在求解非线性方程过程中，控制变量的变化是很必要的，这就要通过松弛因子来实现，它控制变量在每次迭代中的变化。也就是说，变量的新值为原值加上变化量乘以松弛因子。松弛因子可控制收敛的速度和改善收敛的状况，为1,相当于不用松弛因子；大于1，为超松弛因子，可加快收敛速度;小于1，为欠松弛因子，可改善收敛的条件。
   
      本节中对涡轮增压器压气机非定常流动的模拟，压力修正采用SIMPLC算法。为了克服假扩散，对流项采用具有三阶精度的QUICK格式离散，扩散源项采用二阶中心格式离散，时间项采用二阶隐式格式离散。
   
      由于叶片在叶轮内沿圆周均布且认为转速恒定，所以叶轮流道和蜗壳之间呈周期性关系，在计算中时间步长确定如下：

 2.6.6非定常流场计算结果及分析
    应用Fluent软件对涡轮增压器压气机非定常流场进行模拟，计算完成后压力分布结果如图2-23一图2-26所示。

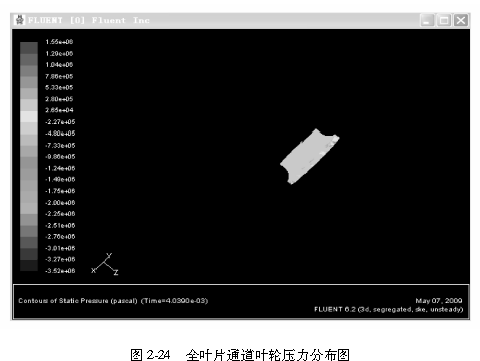
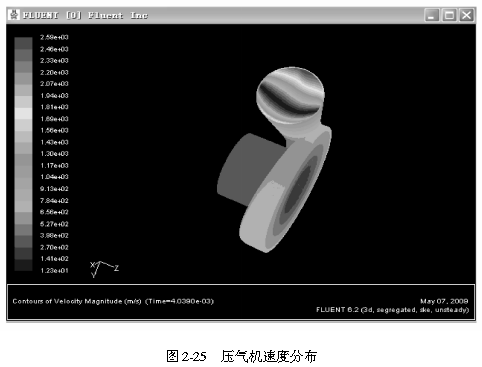
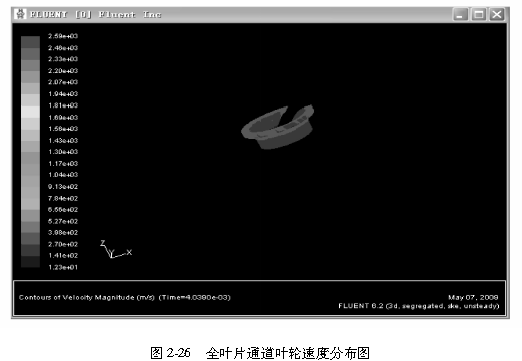
      计算100个时间步长后，得到的静压场分布规律为:从扩压器进口到蜗壳出口，静压压力不断升高，而从进气口至扩压器人口段静压值逐渐下降。
   
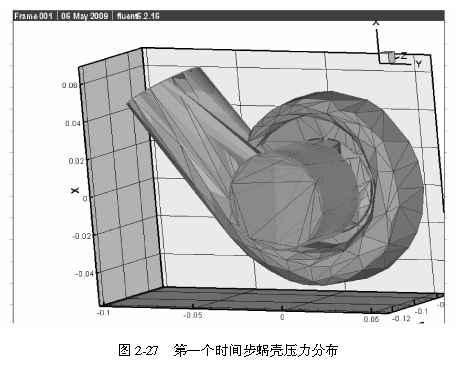
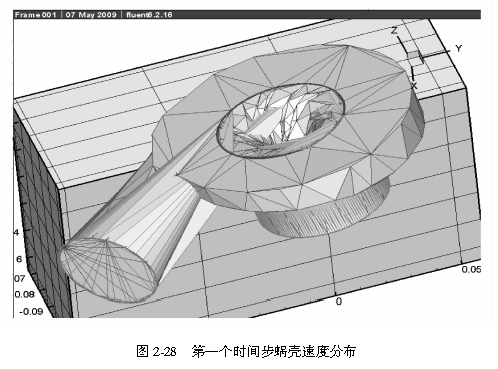
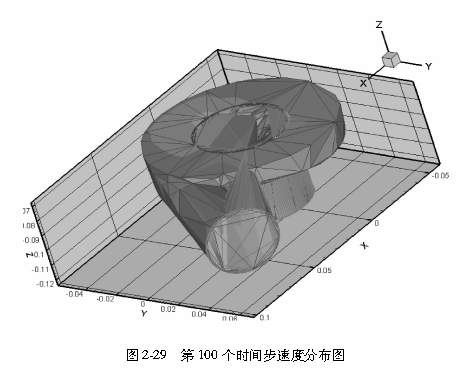
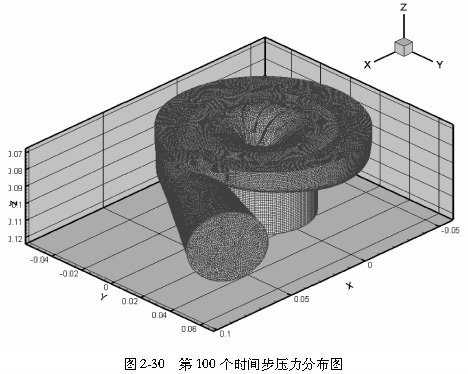
      通过流场非定常计算，导出每个时间步固壁表面、叶轮和叶片的速度、压力值，为随后噪声预估提供数据。在使用FLUENT计算流场时，输出数据文件，并用专业后处理软件Teeplot对每个时间步的流场特性进行处理。利用teeplot软件导出各时间步长的计算结果如图2-27~~图2-30所示。由teeplot中导出的文件转化为.txt文件如图2-31和图2-32所示。