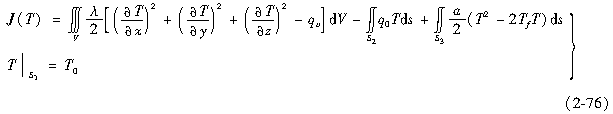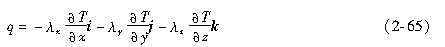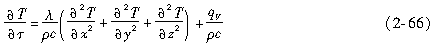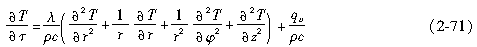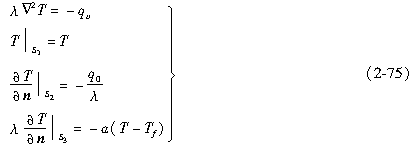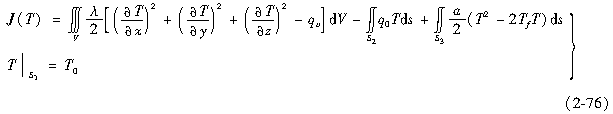第二章 第2章 缓速器设计理论基础

      由温度不同的物体构成的系统，将通过传导、对流和辐射三种方式进行热量传递，形成该系统的温度场。热传导又称导热，是物体各部分没有相对位移或不同物体之间直接接触时，依靠物质内分子、原子或电子等微观粒子的运动，将能量从高温区传至低温区的现象；热对流是发生在流体与固体壁面接触处，除了紧靠固体壁面的一层流体中产生热传导现象外，在流体内部因冷热部分密度差异而引起流体各部分之间相对位移的同时发生热量的转移；热辐射是热源通过流体向其周围非接触传递。

2.3.1稳态导热基本定律

      温度场计算方法目前通用的是热路法和场数值计算方法，采用解析法求解一般很难实现。但描述温度场的解析式能更深刻地反映温度场问题的物理本质，也是数值迭代法解算温度场问题的基础，因此以下首先简述温度场基本方程及导热微分方程，在此基础上给出温度场单值性条件和边值问题。

      Fourier热定律指出，单位时间内通过单位给定截面传导的热量，正比于该截面的温度变化率。它描述热流密度、温度梯度和导热系数之间的变化关系，是导热现象的基本定律

式中，q为热流密度（W/㎡);λ为热导率［W/（m·K)］；T为物体温度（K)。

      直角坐标系中，Fourier导热定律形式如下

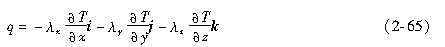
式中，λ_x、λ_y、λ_z为热导率分量。

2.3.2导热微分方程

      对一个无质量变化的封闭系统，设物体是各向同性的连续介质，导热系数、比热、密度等不随温度而变化，物体含有内热源，则根据热力学第一定律和Fourier导热定律，可得导热微分方程的一般形式为

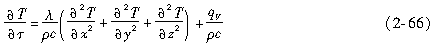
或

式中，T为场中任一点温度，a为热扩散率，且a=λ（cρ)，其中λ为热导率；c为比热容；ρ为密度；q_V为单位体积和时间内所发出的热流量。

      对于3D非稳态无内热源温度场，在直角坐标系下其导热微分方程简化为

      对于3D稳态无内热源温度场，在直角坐标系下上式可进一步简化为3D Laplace方程

或

      以上述两式为基础，可导出1D、2D温度场问题在直角坐标、极坐标和球坐标系的不同形式。当所分析的对象为轴对称物体时，导热微分方程采用柱坐标（r，φ，z)形式如下

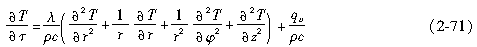
2.3.3温度场单值性条件

      与描述其他物理场的控制方程一样，导热微分方程的求解需要单值性条件，即初始条件和边界条件。初始条件指在初始状态下（如t=0时)的温度值，即T（x,y,z,t)=T₀（x,y,z,t)。

      温度场的常见边界条件分为三类，如下所述。
      （1）第一类边界条件：给定任何时刻物体边界的温度值，即

式中，S₁为边界面；T0为给定温度。
      （2）第二类边界条件：给定任何时刻物体边界面上的热流密度值，即

式中，S₂为边界面；q₀为给定的通过边界S₂的热流密度，当q₀为常数时是恒流边界，当q₀=0时是绝热边界。
      （3）第三类边界条件：给定边界面周围流体的温度Tf和散热系数α。根据牛顿散热公式，物体边界S₃与流体间的对流换热量可写成

式中，T为物体边界温度值。根据Fourier定律，第三类边界条件可写为

式中，Tf为流体的温度，可以是常数，也可以是某种随时间和位置变化的函数；α为散热系数，可以是常数，也可以是某种随时间和位置变化的函数。

      这里，当T>T_f时表示物体散热，当T<Tf时表示物体吸热，当T=Tf时则成为第一类边界条件。

      三类边界条件中，第一类是强制边界条件，第二类、第三类是自然边界条件。

2.3.43D稳态温度场边值问题

      温度场的导热微分方程和单值性条件一起构成了温度场的边值问题。根据上述讨论，对于各向同性介质的3D稳态温度场，其边值问题为

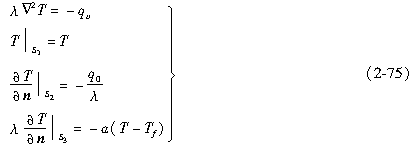
式中参数意义同前。

      上述边值问题的等价变分为