

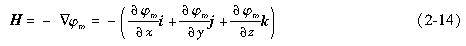
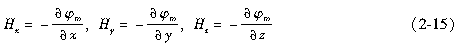
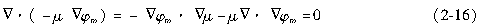
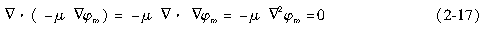



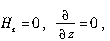 上述结论简化为
上述结论简化为
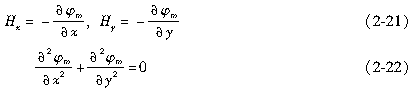

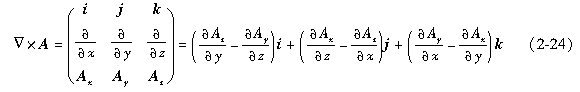
可得矢量磁位表达的磁通密度的具体形式为
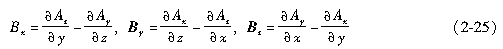
对稳态场由安培环路定律的微分形式(Δ×H=J)和各向同性线性媒质构造方程(H=B/μ),有Δ×B=μJ。将矢量势代入,得双旋度方程

应用矢量恒等式:Δ×Δ×A=Δ(Δ·A)-Δ2A,则有
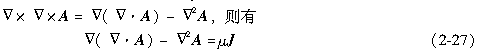
对A的散度施加约束:Δ ·A=0(库仑规范),上式成为

或写成

上式表明,矢量磁位满足Possion方程。
在直角坐标系中,上述矢量形式的Possion方程的形式为
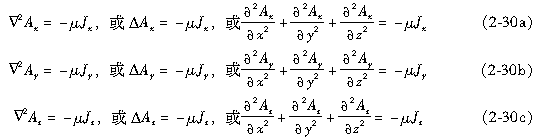
同样,如果磁场可作为2D场,则由于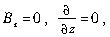 此时上述结论简化为
此时上述结论简化为
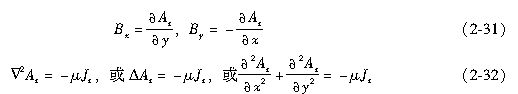
2.2.3边界条件和边值问题——定解条件
分析与计算电磁场的工作有两部分:选定位函数,建立求解区域的微分方程;确定边界和边值条件,以给出方程的定解条件,最后得出待求问题的数学模型。前者在上节中已作叙述,以下讨论边界条件和边值问题。
1、位函数微分方程的定解条件
待求位函数u(标量磁位φm、矢量磁位A)的偏微分方程定解问题有三种类型:仅含初始条件的定解问题为初值问题或柯西问题,无初始条件、只有边界条件的定解问题为边值问题,既有初始条件又有边界条件的定解问题为初边值问题或混合问题。初始条件与边界条件的一般数学描述如下:
(1)初始条件给出初始瞬间u在场域各处的值和对时间的变化率,计算公式如下
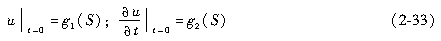
(2)边界条件给出场函数在边界上满足的相关条件,有三种类型:
1)Dirichet问题。给出u在场域边界S上的定值,计算公式如下

前者称为第一类边界条件,后者称为第一类齐次边界条件。
2)Neumann问题。给出u在场域边界S上的法向导数值,计算公式如下

同样,前者称为第二类边界条件,后者称为第二类齐次边界条件。
3)Robin问题。给出u在场域边界S上与其法向导数线性组合的定值,计算公式如下
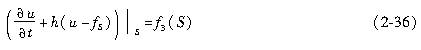
称为第三类边界条件。
2、边界条件的具体形式
(1)不同媒质分解面的边界条件涡流制动型缓速器结构中包含具有不同磁导率的铁区、空气区、线包区等介质。Maxwell基本方程的微分形式只适用于磁媒质内部,即场矢量连续变化的区域。在不同磁媒质分界面上,由于存在磁化面电流,场矢量在分界面两侧将发生突变。可由基本方程的积分形式导出磁场和电场在分界面上的边界条件如下:
场量形式表达如下
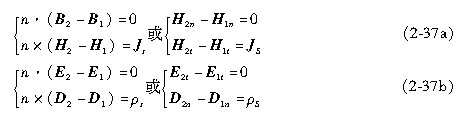
位函数形式表达如下
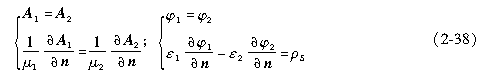
式中,JS为面自由电流密度(或称电流线密度),其方向与沿H2t绕行的方向符合右手螺旋法则;n、t为分界面的单位法向量和单位切向量。
上式表明,在分界面两侧,磁通密度的法向分量保持连续,而磁场强度的切向分量产生突变(矢量场的面散度源可能引起场的法向分量突变,面旋度源可能引起场的切向分量突变。如无磁偶极矩存在,则无散场的法向分量一定连续,无旋场的切向分量一定连续。对调和场,则两种突变均不存在)。
对于各向同性的磁场媒质来说,如分界面上不存在自由面电流,则处在分解面两侧的B矢量和H矢量服从折射定律,即

式中,α1、α2分别是在两种媒质在分界面处的法线与B、H矢量之间的夹角。
显然,由于在铁磁性材料与非铁磁性材料的分界面上有μ1>>μ2,这时只要α1≠90°,而α2≈0°,即可近似认为在非铁磁性材料的一侧靠近分界面处,B、H矢量垂直于分界面。
(2)无穷远处的边界条件当场域无界时,定解条件还包括无穷远处的边界条件。场源分布在有限区域内的无界场问题,场函数在无穷远处取值为零:ur→∞=0。
3、边值问题
上述位函数的泛定方程和边界条件一起,构成了边值问题,是待求物理问题的数学模型。在平面线性稳定电磁场中,标量磁位、矢量磁位的边值问题分别为
1)标量磁位
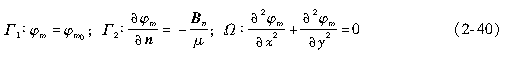
2)矢量磁位
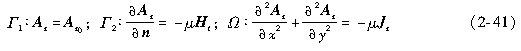
统一写成
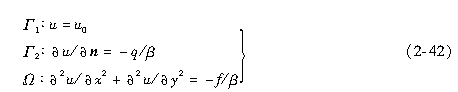
统一形式的泊松方程的边值问题与物理量的对应关系列于表2-1中。

2.2.4磁场能量与电磁力
1、磁场能量
在n个线圈回路的磁场中,磁场能量表达为

式中第k个回路的磁链为

所以n个线圈回路的磁场能量可表示为

当电流分布在媒质内,则由于JdV=IdI,上式可写为

根据Maxwell方程,上式可写为

根据前述矢量积的散度公式A·Δ×H=Δ·(H×A)+H·Δ×A,上式又可写为
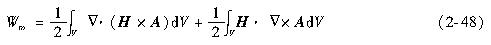
应用高斯定理及B=Δ×A,上式成为
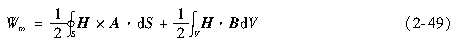
当积分扩展到无穷远处时,上式第一积分项为零,这样

磁场能量的体密度为

而对各向同性的线性媒质,磁场能量的体密度为

以上是线圈电磁场磁场能量和磁场能量体密度计算公式的导出过程。
2、电磁力
磁场能量以力和力矩形式应用于涡流制动装置中。磁场无论是由永磁体产生的还是由载流线圈产生的,由于运动电荷磁效应的作用,都将在磁场中产生两类磁场力或力矩作用,即载流导体在磁场中所受的磁场力和磁介质在磁场中所受的磁场力,有些文献分别称之为洛伦兹力和磁阻力。前者主要应用于电机、电磁仪表等设备和仪器中,后者则主要应用于各类永磁或电磁型磁力机械中。机器中应用这两类力及产生的力矩可实现能量转换、动力执行、运动传递等功能。
(1)Lorentz力磁场对运动电荷产生的作用力为df=q(V×B),载流导体在磁场中所受到的力是导体内自由电荷所受力的总和。导体电荷体密度为σ,则q=σdV,而J=σv,所以df=σdV(V×B)=dV(J×B)。这样,单位体积载流导体受力(力密度)为

当载流导体为线状时,电磁力为

洛伦兹力公式表达了电动机和一些电磁仪表的基本工作原理。
(2)磁阻力介质在磁场中所受的磁场力(磁阻力)实质是磁场对介质磁化电流(分子电流)的作用。磁性介质磁化电流的体密度为Jm=Δ×M,在介质表面存在表面磁化电流,其面密度为JS=-n×M。式中,M为介质的磁化强度,n为表面法向矢量。按上述电磁力计算公式,可得磁场对介质的作用力为
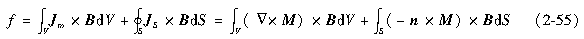
对于各向同性介质,上式可简化为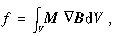 磁场力的体密度为f=MΔ B。由于
磁场力的体密度为f=MΔ B。由于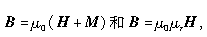 可得
可得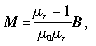 从而磁场对介质作用力的体密度为
从而磁场对介质作用力的体密度为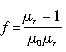
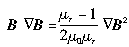 。
。
考虑介质中还有传导电流时,由于传导电流受力的密度f=J×B,因而总的力密度为

对于线性介质,设ρ为介质密度,则上式成为
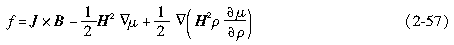
上式物理意义如下:J×B为传导电流受力;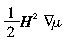 为磁介质内部和交界面处的μ的不均匀性引起的力,方向由μ值大处指向μ值小处;
为磁介质内部和交界面处的μ的不均匀性引起的力,方向由μ值大处指向μ值小处;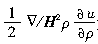 为磁介质内受力后发生变形使μ发生变化引起的力,通常称为磁致伸缩力。
为磁介质内受力后发生变形使μ发生变化引起的力,通常称为磁致伸缩力。
Faraday认为磁场中磁通管有沿纵向和横向的张力,两者大小相等,力密度为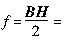
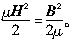 按此方法求解电磁力有时也称为Maxwell应力张量(MAXWELL STRESS TENSOR,以下简称MST)法。
按此方法求解电磁力有时也称为Maxwell应力张量(MAXWELL STRESS TENSOR,以下简称MST)法。
另一种求解电磁力的方法是虚功(VIRTUAL WORK,以下简称VR)法。在n个线圈回路的磁场中,第k个回路的电流为Ik,磁链为ψk,当第i个回路在某一广义坐标上有虚位移dx、其他回路不动时,电源输入回路系统的净电能dWe应等于磁场储能的变化dWm与机械能的变化dWΩ之和,计算公式如下

式中,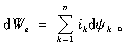
而机械能的变化为磁场力所做的功,设第i个回路的磁场力为fi,则dWΩ=fidx。代入上式中,得磁场储能的变化为

即磁场储能是独立变量ψ、x的函数,其表达式为
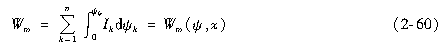
式中,ψ=(ψ1,ψ2,…,ψk,…ψn)。将Wm表达为全微分形式为
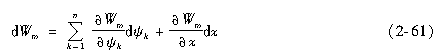
将其与磁场储能的变化式比较,可得

上式就是以ψ、x为独立变量表示磁场储能时磁场力的表达式。
当虚位移为角位移dθ时,磁场力变成磁场力矩

ICP经营许可证:鄂B2-20080078
(于2003年首获许可证:鄂B2-20030029)
鄂公网安备:420100003343号
© 2002-2025 武汉制信科技有限公司 版权所有
投诉举报电话:027-87592219