第二章 轻量化材料

    设计材料的种类（金属、陶瓷、聚合物与复合材料）本质上是按照原子结合的方式来进行分类的，原子的结合方式决定了材料的主要性能。本节阐述了材料直至弹性极限的弹性变形能力，并给出了以重量为基准的比材料参数的定义，该定义也与材料的价格相关。从金属的塑性变形能力出发，引出了强化机理。根据这一机理，材料的屈服强度可以在更大的区域范围内变化。温度升高是材料产生扩散过程的原因，并会在弹性极限内引发蠕变变形。弹性区域和接近屈服强度区域的交变载荷会使材料产生损伤，从而极大地限制材料的使用范围。断裂韧度则限制了材料的允许应力与缺陷大小，特别是陶瓷材料的允许应力和缺陷大小。磨损与腐蚀可使材料产生损伤，从而降低材料的持久承载能力。为了能够对轻量化材料进行评估，将材料的机械承载能力极限与密度联系起来。材料的性能由成形方法与后续加工确定，因此，材料的选择是一个整体的过程，包括了结构设计、材料要求、成形方法、经济使用以及生态影响。
2.1.1引言
    在20世纪的后半叶，材料的种类急剧增加。据估计，目前用于产品加工的材料有10万种之多。基本上，材料可以分为金属、陶瓷与塑料，由这些材料还可以组成复合材料。与采用连接技术生产的材料复合物不同（见4.2节），对复合材料可以理解为，材料宏观性能的表现如同均匀材料的性能。工程材料必须要能够承受载荷（表2.1.1），特别是机械载荷［5］。另外，还有环境的载荷，如温度和腐蚀性介质。需要注意的还有加工过程中产生的与外界载荷叠加的材料内应力。表2-1-1给出了最重要的检测方法、特征值及其符号，它们表征了材料的性能。在轻量化中，必须在尽可能小的重量下，满足设计所要求的材料的使用性能。

    随着工业中所采用的各种材料的不断增加，在构件的混合构造中也产生了各种不同的应力载荷（见4.2节）。图2-1-1所示为一款轻量化轿车中各种材料所占的比例［6］。示例中，轻量化材料占据了超过整车一半的重量，其中塑料和轻金属的比例差不多。汽车上要求高强度的区域则采用钢材制造。铁基材料（钢和铸铁）所占重量为轿车总重量的三分之一。轻量化材料所占的比例可以由图中所示的质量分数看出来：聚合物的体积分数超过轻金属的两倍，轻金属的体积分数又超过了铁基材料体积数的两倍。

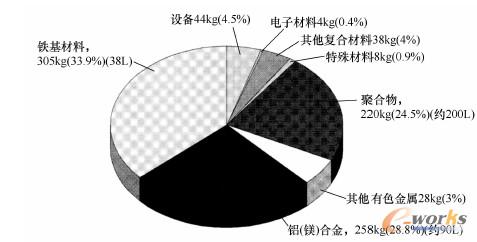
图2-1-1轿车中材料的多样性示例（奥迪A2，制造年份：2000年），净重900kg［6］

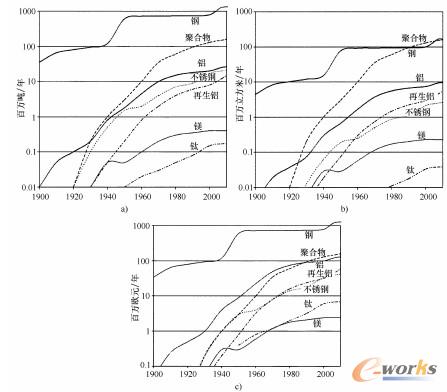
图2-1-2在过去一百年里，工业材料产量的发展状况

a）每年的重量b）每年的体积c）每年的市场价值

    材料的意义不仅取决于可生产出的材料的重量，也取决于可生产出的材料的体积，更取决于材料新创造出的价值。图2.1.2所示为过去一百年来工业材料的增长情况。在20世纪前半叶，材料产量增加了25倍，在20世纪的后半叶则又翻了一番。目前所生产的塑料的总重量只比钢的重量总量低一个数量级，但是按照体积计算，二者是相同的。塑料与铝材料新创造的价值差不多，但是比钢新创造的价值低一个数量级。再生铝生产比原生铝的增长要晚15～20年（见5.1节）。在图2-1-2中，镁和钛则比位于其上面的材料低几个数量级。下面对材料最重要的力学性能作简要的介绍，关于材料力学性能更详细的内容可以参见与材料技术基础相关的文献［1～5］。
2.1.2材料种类
    材料的密度取决于原子的质量和原子的堆积密度。塑料由轻的元素（碳、氢、氧、氮）构成，元素通过分子链的强烈共价键结合而成，而分子链则通过弱的二次键连接。同样，陶瓷也是由金属元素与轻元素硼、碳、氮、氧的共价键分子构成的。轻的陶瓷分子通常也是相互共价结合，与电静态离子键部分连接。金属元素的正离子在晶体结构中呈三维周期性排列，通过电子气体连接，其密度主要由原子的质量确定。轻金属主要是指镁基合金［7］、铝基合金［8］与钛基合金［9］（密度<4.6g/cm3）。元素的原子半径表示了与周期系序列相对应的振荡（图2-1-3）。图中标明了在钢、镁合金、铝合金和黄铜中的合金元素。材料的种类基于不同的键类型，如图2-1-4所示。聚合物分子绝大多数是不规则的（非晶的），图2-1-4键的类型影响到材料的性能［3］但是可以按照区域有规律地排列（结晶的）。陶瓷和金属或者是非晶的（玻璃状的），或者是结晶的。图2-1-5a和图2-1-5b对自然界中常见的最紧密堆积的原子排列方式进行了比较。图2-1-5c所示为不太紧密堆积的体心立方晶格结构。除了若干例外，结晶材料都是由具有不同结晶方向的晶体构成的，晶体的直径在微米到毫米的范围内。一般来说，材料都是多晶的。

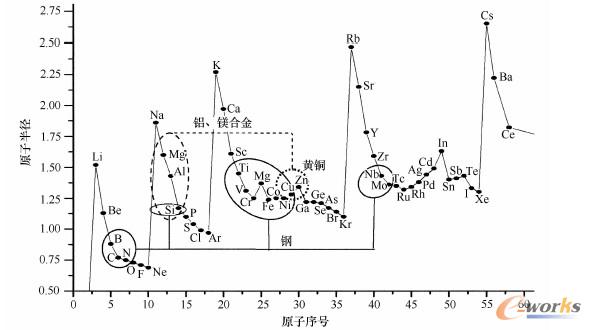
图2-1-3原子半径取决于顺序数。在钢中，小的原子如硼、碳、氮占据了铁晶格的中间晶格位置，而其他元素作为替代原子被吸收了。元素在铝合金和镁合金中只作为替代原子出现。黄铜（铜–锌）可以达到非常好的固溶强化效果

    键的类型和原子排列构成了材料的物理和力学性能基础：聚合物和陶瓷导电能力和导热能力都不如金属。键结合越强，材料的熔点和弹性模量越高，热膨胀系数越小。这些参数之间的内在关系可见图2-1-6。

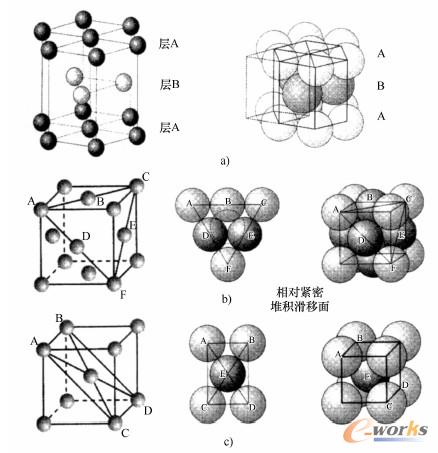
图2-1-5常见简单晶体结构

a）最紧密堆积基准平面（Mg,αTi）的密排六方晶格结构（hdp）

b）最紧密堆积对角平面（Al、γFe、Cu、Ni、Ag、Au）的面心立方晶格结构（kfz）

c）相对紧密堆积对角平面的体心立方晶格结构（krz）（αFe、βTi）

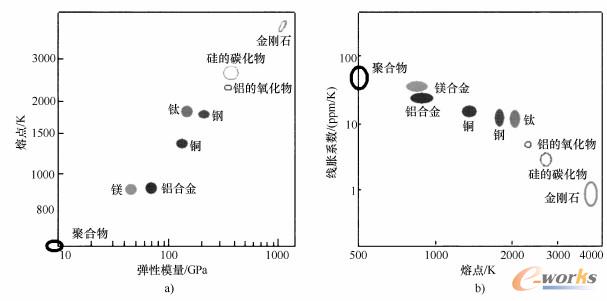
图2-1-6聚合物的熔点和气体过渡温度与下列参数之间的内在关系

a）弹性模量b）线胀系数

2.1.3弹性性能
    材料的弹性性能基于原子间的键合力（图2-1-7）。在原子位置上，吸引力和排斥力处于平衡状态。由原子力径向曲线的切线可得出弹性模量，在胡克定律［方程式（2.1.1）］中，弹性模量将弹性应变ε与要求的应力σ联系起来：

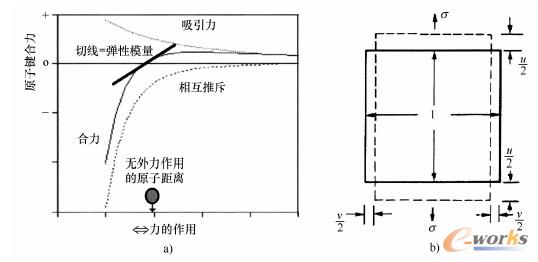
图2-1-7示意图

a） 两个原子之间的结合力，为推斥力与吸引力作用的结果。由原子平衡位置上的切线可得出

弹性模量。吸引力越大，切线越陡峭，弹性模量上升幅度越大b）在压应力σ下随着弹性伸

长u下出现的固体弹性横截面减小ν，用于解释泊松比ν，见方程式（2.1.1）

    在横向收缩（v）的拉伸方向（u）上，采用泊松比ν来描述弹性应变的轻微不对称性（图2-1-7b）。泊松比只在弱连接的合成橡胶中接近0.5，这表示体积为常数。绝大多数情况下，泊松比小于0.5，这意味着，在弹性变形下体积会发生膨胀。在很强的陶瓷结合中，泊松比约为0.2；在金属和热固性塑料中，泊松数约为0.3；在泡沫结构中，泊松比可以接近零。
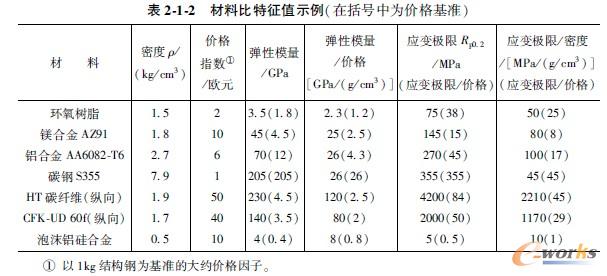
    表2.1.1给出了以重量为基准的弹性模量和弹性极限等材料性能。将特征值除以密度，可得出材料的比弹性模量和比应变极限。碳纤维与碳纤维增强塑料 （CFK） 在纤维方向上的比特征值高于其他的材料。表中列出的实体金属的比弹性模量大致相同。通过除以价格指数的方式，突出了针对弹性模量的相对价格。价格指数表示了对于钢的材料价格的倍数［10］。由表2.1.2的例子中可看出，对于弹性模量、屈服强度特征值及以重量为基准的参数值来说，钢具有价格最低的特征值。
 

    结构的弹性变形取决于几何形状和载荷的多轴性，可以用刚度来描述。图2-1-8所示为一端固定的金属桁梁的刚度：由密度不同的材料构成的桁梁，在重量相同的情况下，厚度不同。轻量化材料具有更高的刚度。桁梁的密度越小，在相同的刚度下，桁梁越轻。采用特别轻的试验材料镁锂合金（ρ=1.4g/cm³）［11］可制造出最轻的、刚度最大的桁梁。在相同的刚度下，钢桁梁的厚度最薄，即使是这样，它也是最重的，是镁锂合金桁梁重量的三倍。

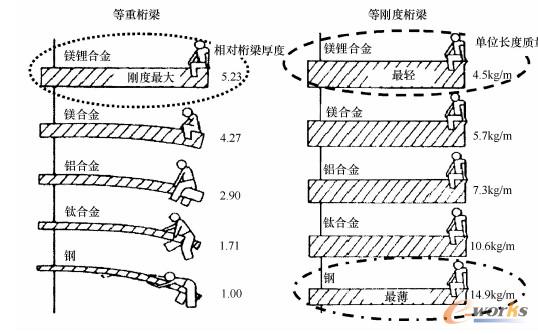
图2-1-8由各种金属构成的刚性桁梁的图示比较（镁锂试验合金密度为

ρ=1.4g/cm3［11］）：密度最小的材料刚度最好、最轻，桁梁也最厚。

    弯曲载荷的材料效率由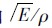给出，可以看出，轻质材料的效率更高（见2.3节）。类似地，密度为ρS的泡沫结构的刚度S取决于实体材料密度比例的平方：S/E=c（ρS/ρ）²［12］。低密度的材料只有用于弯曲载荷和扭转载荷，才可以有效地利用材料所具有的高刚度。
    通过陶瓷植入（增强），可提高聚合物和金属的弹性模量。复合材料的刚度则取决于增强材料的布置和体积分量vf。根据方程式（2.1.2a），可沿着纤维增强方向以及垂直于纤维增强方向达到有效弹性模量E的极限值。根据相同应变与相同应力的边界条件，可按照图2-1-9求出有效弹性模量E的极限值。指数f和m与增强材料（如：纤维）和基体有关。
 

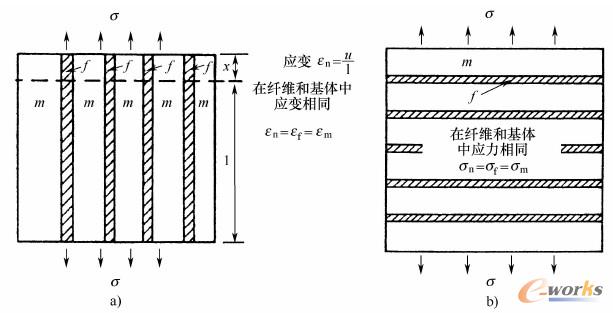
图2-1-9用于复合材料的混合规则方程式（2.1.2a）的求导

a）在相同的纵向弹性应变下，根据Voigt规则

b）在两个组件相同的横向应力下，根据Reuss规则［1］

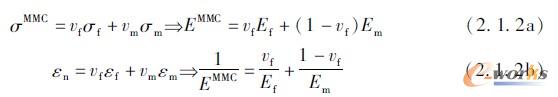
    根据Voigt［方程式（2.1.2a）］的线性混合规则可得出材料纵向刚度的上限值；而根据Reuss［方程式（2.1.2b）］的交互混合规则,可由连续应力得出材料的下限值，这也适用于颗粒增强的材料。图2-1-10表示了由方程式（2.1.2a）得出的材料极限值：E=230GPa的各向同性纤维以及横向弹性模量只有10GPa的各向异性碳纤维。由此可得出材料在整个体积分量区域分布的极限值。碳纤维增强（见22节）在横向上总是与增强功能配对（在金属基体中，碳纤维在横向上刚度减小），而增强功能对于塑料基体来说是可以忽略不计的。按照线性混合规则，可通过计算得出复合材料的密度。因此，通过刚性植入陶瓷可提高材料的比刚度，进而提高材料整体的比弹性模量。以此类推，可将混合规则用于其他的性能，来考察适用于复合材料的合适组件［13］。

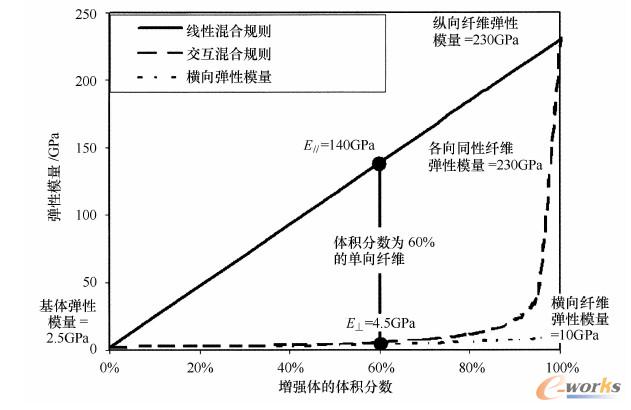
图2-1-10针对单向碳纤维复合增强塑料的纵向与横向弹性模量的混合规则示意图（见表2.1.2），纤维弹性模量为各向异性或者假设纤维弹性模量为各向同性（例如对于陶瓷纤维）

2.1.4强度与塑性变形
    一般来说，材料只允许在弹性极限以内承受机械应力载荷，构件在使用的时候不允许发生塑性变形。但是在加工时，为了便于构件成形，会利用金属和热塑性塑料的延展性。图2-1-11所示为拉伸试验的应力应变曲线图，从曲线图中可以得出以下特征值：根据方程式（2.1.1）由胡克直线得出的弹性模量；通过x%屈服强度（即：Rp0.2）定义的实际弹性极限，即允许发生x%的塑性变形（即：0.2%）；均匀塑性变形区域，有至最大强度（Rm）及其应变（Agl）的强化过程；然后是由材料损伤导致的弱化过程，直至在断裂伸长率下材料发生断裂。卸载会导致与胡克直线平行的回弹。图2-1-12显示了各种材料的不同应力——应变曲线变化过程：脆的碳纤维和硬化钢具有高强度，但无塑性变形；奥氏体钢和热塑性塑料具有特别大的塑性变形；而位于中间的铸造材料和变形材料则有不同的塑性变形行为。铁素体钢的屈服强度显示出了特殊性（见图2-1-12中的曲线1、2和4），即在超出屈服强度之后还有一小块未强化的变形区域。在表2.1.2中列出了一些材料的屈服强度和比屈服强度。铝镁硅变形合金的比屈服强度［8］略高于其他金属的比屈服强度。具有高强度的结构钢的成本最低，但是具有最高比强度的碳纤维也不是更贵。在2.3节中比较了各种应力载荷状态下的以重量为基准的强度值。

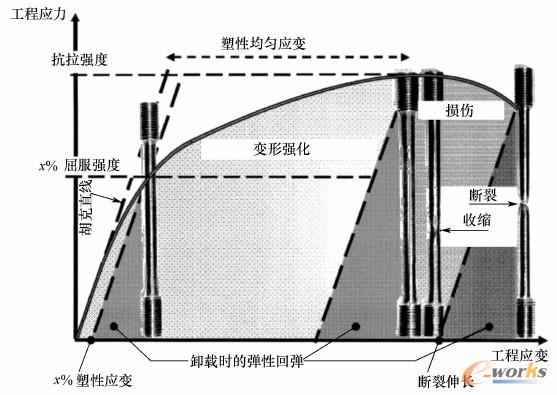
图2-1-11塑性金属的工程应力–应变工艺曲线，通过带有弹性、均匀塑性和局部（损伤的）变形区域的变形拉伸试样得出。图中显示了拉伸试验特征值x%屈服强度、抗拉强度、均匀应变与伸长率。弹性回弹取决于应力下降的大小。

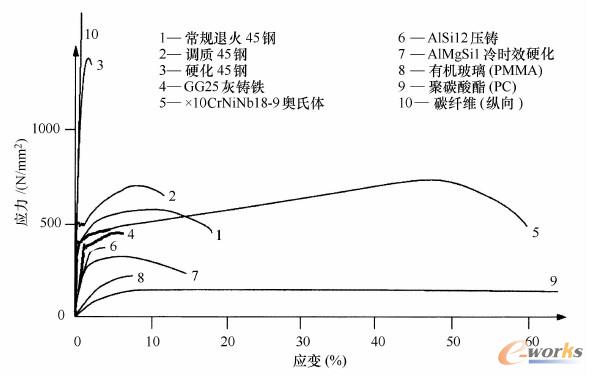
图2-1-12钢、铸造合金、铝变形合金、热塑性塑料和碳纤维（代表了陶瓷，线弹性断裂在图表区域之外，见表212）的典型拉伸试验曲线。铁素体材料（曲线1、2、4）显示出屈服强度［2、5］

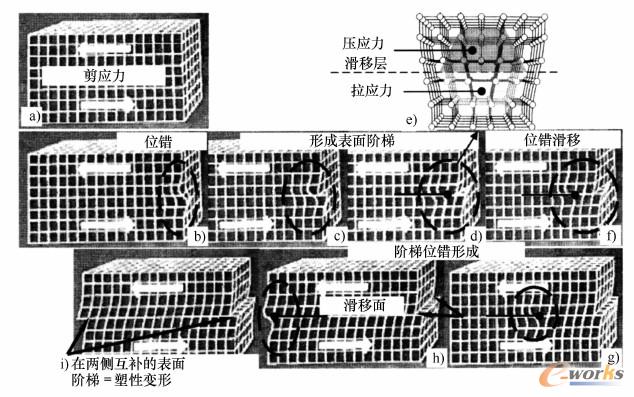
图2-1-13由位错滑移导致的晶体塑性变形示意图

a）完美晶格b）剪切应力在接近表面处产生扭曲

c）表面上的阶梯d）内部位错形成e）带有压/拉应力区域的阶梯位错

f、g）位错伴随扩展的键交变h）位错达到晶体另一侧的滑移面

i）位错离开。留下相对的阶梯，表示在晶格周围的塑性变形

    金属的塑性变形可归因于线形位错的运动。在晶格中，等价离子占据了晶格位置，因此在滑移面（相对紧密堆积晶面，见图2-1-5）上，晶格结合的位移只需以很少的变形能进行，而不破坏晶格连接。图2-1-13所示为带有局部弹性位错的阶梯位错的片断。如图2-1-13a中所示，剪应力推动位错，直至位错横穿过晶体区域产生了塑性变形。当剪应力大到将位错不可逆地推动穿过晶体时，则剪应力达到了弹性极限。内部应力场可以阻止位错运动，从而提高弹性极限，实现强化效果。图2-1-14所示为合金化带来的一些晶体缺陷：不同大小的溶质原子（图2-1-3）或者新成形的晶粒（析出），如图2-1-14c所示。围绕着这些晶体缺陷的应力场起到固溶强化以及析出强化的效果，这种强化的效果越大，晶粒越是紧密地位于晶核的周围。图2-1-15表明了，晶体缺陷是如何阻碍了位错的运动，以及与障碍有关的剪应力定性变化过程。

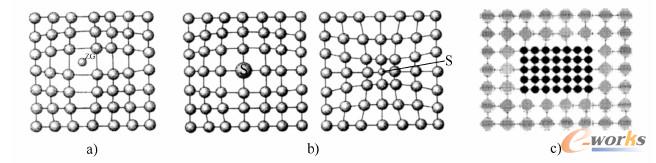
图2-1-14晶格中的溶质原子产生内部应力场，从而阻碍了位错的滑移：点缺陷如

a） 晶格间原子（ZG）b）更大的与更小的替代元素Sc）溶质原子三维排列（析出）

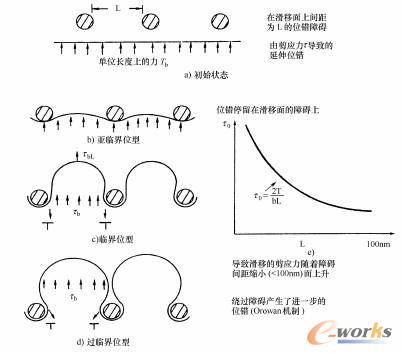
图2-1-15克服周期性不可切割的障碍以实现位错滑移运动的示意图。

    缺陷平均距离越小，借助Orowan机制所需要的克服障碍的剪切力越大［1］金属的塑性变形产生新的位错，位错密度会提高，从而使得位错相互之间的运动受到阻碍。这样就产生了应力应变图中所见到的变形强化结果。晶体变小也可以提高临界剪应力，从而导致了细晶硬化效果。不过，即使是细晶硬化也无法阻止延展。而在纳米级别的颗粒中，则不会再有位错运动了（高强度、低延展性）。
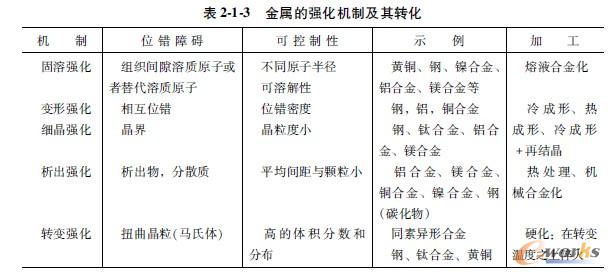
    图2-1-16所示为铝及铝合金的强化方法［8］：不可时效硬化铝合金采用固溶强化和变形强化的方法，可时效硬化铝合金除了以上两种方法之外还可以采用析出的方法。强化机制对弹性模量没有影响，只有弹性极限可以提高很多倍。一般来说，强化的同时还阻碍了变形（Agl）。同素异形金属如铁和钛的转变硬化对位错运动的阻碍特别大。通过淬火抑制平衡转变可形成带有扭曲晶格的不平衡状态（即马氏体），使临界剪应力大大增加。图2-1-17所示为在高强度碳素钢中的针状马氏体。表2.1.3总结了金属的强化机制，并列出了如何在不改变密度和弹性模量的情况下，从根本上改变弹性极限的示例。通过改变晶粒大小可以将铝和钢的比强度提高十倍以上。在2.3节中的图2-3-3表示了材料强度区域与比重的关系。

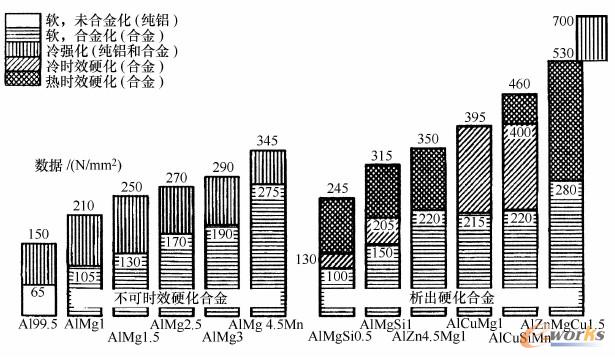
图2-1-16用于铝合金的强度提高方法：不可时效硬化处理合金的固溶强化和变形强化；在析出强化合金中的附加冷强化以及热强化

    采用碳纤维和陶瓷纤维，塑料和轻金属可以通过应力移位得到增强。纤维具有高弹性模量，承受了在纵向上的应力，减轻了基体材料所承受的载荷。图2-1-18所示为单向连续纤维增强铝合金（A6082/CHT/60fUD，组件特征值见表2.1.2）的应力-应变图。根据线性混合规则方程式（2.1.2a），对在纤维和基体中的应变控制应力相加。两个组件首先都产生弹性应变，可由复合刚度EMMC1给出。在超出基体的屈服强度时发生塑性变形，会使应力—应变曲线产生压弯，压弯斜率由EMMC2标识。一旦出现纤维断裂，则复合材料在RMMCm下失效，从而无法利用直至抗拉强度Rm的基体强化。

图2-1-17在确定结晶方向上，经过马氏体转变后，碳素钢中具有高内应力的针状马氏体。

针状马氏体的密度越高，弹性极限越高，变形能力越小［5］

2.1.5温度升高的影响
    随着温度升高，固体原子间的键合力减弱，原子间距增大，随后弹性模量减小，热膨胀系数增加［1～5］。对于陶瓷材料来说，由于有强烈的共价键结合，性能相对温度比较稳定。在固体内的扩散过程受温度影响很大。随着空穴浓度增加（在晶格中没有被占据的位置），扩散过程会加速进行。方程式（2.1.3）用常数D0和气体常数R表示了扩散系数D的温度指数相关性（热力学温度T，单位为Ｋ）。

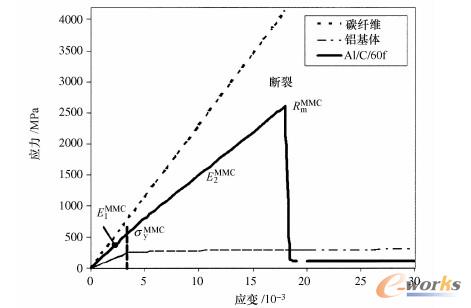
图2-1-18由拉伸试验得出的应力—应变曲线，试样分别为铝基体、碳纤维、单向增强金属基复合材料（CFRM:Al/C/60fUD），沿纤维方向；E^MMC₁和E^MMC₂
为无基体塑性化的纵向刚度和有基体塑性化的纵向刚度；R^MMC_m为最优抗拉强度 

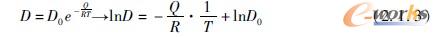
    Arrhenius对数表达式将这些指数函数线性化，其中斜率由激活能量Q给出。从图2-1-19a给出的示例中可以看出，金属中原子运动性是如何的不同：在400℃的温度下，氢（氢核）扩散的速度比钢中的晶格间原子碳的扩散速度快了6个数量级，而铁的置位过程则通常要比晶格间原子碳的置位过程慢将近10个数量级。即使是这样，在温度超过400℃后也可以观察到铁基材料的扩散过程。根据经验规律，对于聚合物来说，在达到超过40%的热力学熔化温度（单位为K）以及在聚合物中达到玻璃过渡温度后，会观察到宏观的扩散过程。由于在陶瓷中不可能发生位错运动，因此只有塑性变形才能产生扩散过程。对于绝大多数的聚合物来说，在室温下就会产生蠕变变形。不过，对于绝大多数的镁合金来说，当温度超过50℃后，也会发生蠕变。对钛合金来说，直到温度超过500℃后才会产生蠕变变形，但是晶格间原子的扩散会使钛合金容易产生腐蚀。

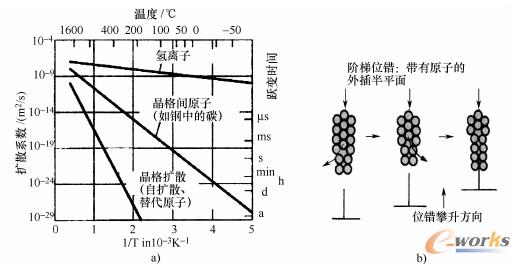
图2-1-19

a）氢离子（氢核）在金属中扩散系数与温度之间的关系等级，给出了带有原子跃进概率（跃变时间）的晶格间原子和晶格扩散［2］b）阶梯错位扩散控制攀升的示意图：原子从外半平面边缘扩散开去，使得错位进入了另一个滑移面

    随着晶体缺陷运动的增加，金属的强化机制会减弱。图2-1-19b显示了一个阶梯位错原子的离散是如何改变原子位置的：离散使得原子“攀升”到了另一个滑移面上，从而绕过了与时间和温度相关的障碍。接下来，随着温度升高，位错在弹性极限内随着时间推移导致了塑性变形，即蠕变变形。图2-1-20a显示了随着载荷时间变化的蠕变应变曲线，图中也描绘出了弹性应变分量。在图2-1-20b中，可以看出由应变时间导出的蠕变曲线上的三个蠕变阶段。

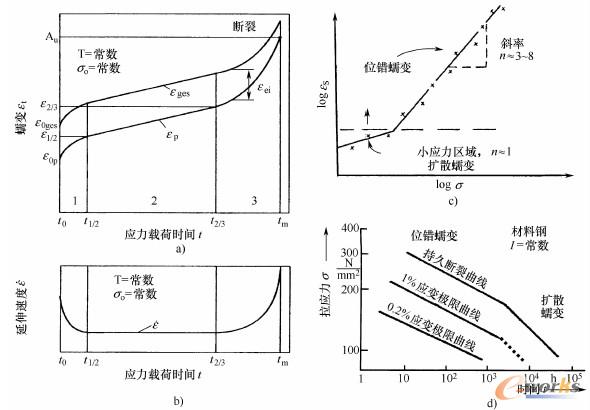
图2-1-20热活化蠕变变形

a）总的应变和塑性应变作为时间的函数（在恒定温度和应力下＜弹性极限）

b）不同应变速度的区别（1）初始蠕变阶段（2）稳定蠕变阶段（3）第三蠕变阶段

c）稳定应变速率按照指数律（Norton定律）随着应力上升而上升d） 持久延伸极限直至达到规定的塑性变形，取决于载荷时间与持久断裂线（持久强度），在一定的时间后产生断裂［1、2、5］

    二次、近静止的蠕变阶段与应力的关系可用Norton蠕变法则方程式（2-1-4）求出。在方程式中，扩散系数表示了温度指数关系。A是与材料有关的常数。对数指数函数的斜率（图2-1-20c）给出了蠕变指数n，蠕变指数与蠕变机制有关。

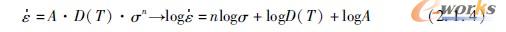
    在低载荷和高温的情形下，主要发生晶界扩散或者体积扩散，对应于n=1；当n=3～5时，位错蠕变（有位错或者位错攀升的溶解合金元素的扩散）确定了蠕变速率。内部应力可通过蠕变机制得到松弛。
    在设计高温构件时，承载性不仅受限于拉伸试验的屈服强度，也受限于更低的x%持久应变极限应力σxt,T，即在一定温度、一定时间条件下，在轴向载荷的作用下，线性材料产生的x%变形（例如：σ1%1000h，800℃）。图2-1-20d显示了在位错蠕变阶段02%和1%持久延伸极限的时间变化曲线。极可能导致断裂的应力可标识为持久强度，作为疲劳曲线绘在图2-1-20d中。疲劳曲线的压弯以及扩散蠕变过渡的1%持久应变极限的压弯清楚地表明了从持久延伸极限外推超出机理极限的危险。要提高合金的抗蠕变性能，可以有两个方法：或者是添加耐高温的位错障碍物，如细小的陶瓷弥散介质（如：粉末冶金方法制造的弥散强化铝合金）［1、5］；或者是通过陶瓷增强件［如：塑料（见22节）和轻金属［9,14］的纤维增强］而使应力重新分配。
2.1.6材料损伤与断裂
    根据拉伸试验可对图2.1.21中所示的断裂种类加以区分。将示意图与金相照片进行比较，可以得出：
    ●无变形解理断裂：无位错运动的、带有光滑断裂面的穿晶裂纹（图a、f）；沿晶界的无变形裂纹扩展（图b、g）。
    ●在脆性收缩上通过孔洞形成的内部裂纹，可以通过在显微照片上的凹坑和尖角（图h）来识别：在晶粒内的韧性变形出现的角（图c）；在晶界上的微韧性变形（也可以在无宏观收缩的情况下发生断裂=脆性断裂）（图d、i）。
图2-1-21i所示为钢拉伸试样在断裂面附近的显微射线照片。照片中显示了孔洞，在断裂面上孔洞的数量急剧增加［15］。
●延展剪切断裂（图e）：在相对纯的金属（含碳量少的结构钢）中，通过沿着与变形方向成45°倾斜角的平面的滑移，导致接近完全的收缩（Z～100%）。

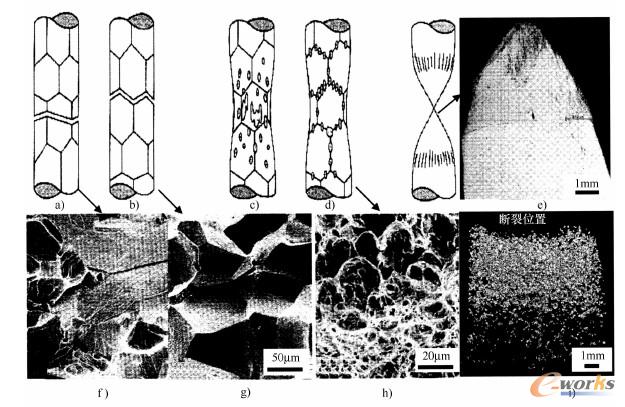
图2-1-21金属断裂类型（以碳素钢为例）

a）穿晶解理断裂，断口显微照片图f（和图g 的放大倍数相同）

b）晶间解理断裂，断口显微照片图g
c）晶内小坑与d)晶间小坑，断口显微照片图h［2］与X射线照片［15］在图i中可看到明亮的孔洞，孔洞数量一直在增加，直至断裂位置

e）带有纵向磨痕和单一孔洞的韧性剪切断口

    当超过抗拉强度（图2-1-11）时，在拉伸试验中看到的韧性金属弱化现象可归因于韧性收缩，其原因则是由于金属存在内部变形孔或者剪切变形。只要存在由加工或者局部变形导致的内裂纹、外裂纹、缺口，就会在缺口根部导致应力集中。在单轴外拉应力σ作用下，由于裂纹区域a不承受载荷，所以裂纹周围必须承受增加的应力，如图2-1-22所示。方程式（2-1-5）可用应力强度因子K来量化，其中f为缺口的形状因子。在裂纹尖峰处，应力可以很高，使得原子间的键合发生撕裂，从而产生无变形的解理断裂。为此，可用相应的线弹性断裂机理［1～5］来定义断裂韧度K_lc：

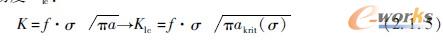
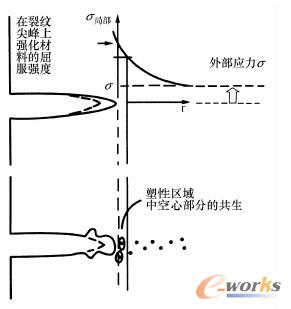
图2-1-22从外表面出发的应力变化和裂纹扩展，与拉伸载荷平行变化：裂纹尖峰处的应力集中随着裂纹长度而增加；或者超出原子间的结合力而导致解理断裂，或者超出材料的弹性极限，从而在强化后导致过载塑性化区域的局部损伤［1］

    断裂韧度是一个材料特征值。断裂韧度现象主要可以在脆性材料和高强度材料中观察到。在这些材料中，会出现高弹性应力。只要在外应力σ作用下，达到临界裂纹长度 a临界，材料就会发生解理断裂，这种情形下出现的最大应力为弹性极限。在韧性材料中，在裂纹尖峰处出现的应力集中可通过塑性变形来消除。如图2-1-22所示，裂纹可通过提前形成的凹坑（如同在拉伸试验中）得以扩展，从而导致韧性断裂。一般来说，根据方程式（2-1-5）得出的材料比韧度表示了材料应力载荷的另一个极限。
    基于线弹性断裂机理，不会产生塑性变形的材料（陶瓷、玻璃、热固性塑料、淬火钢）会由于解理断裂而发生突然断裂。这些材料的强度取决于加工条件下内部缺陷的分布（图2-1-23a）。内部缺陷的分布可借助魏布尔统计方法根据方程式（2-16）来描述［1］。

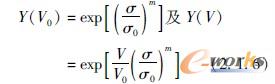
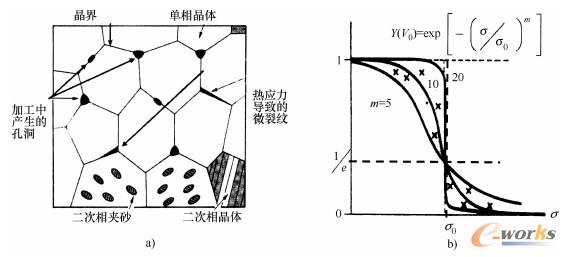
图2-1-23

a）非塑性化材料（陶瓷、热固性塑料、淬火钢）的断裂失效取决于缺陷分布

b）强度模数σ0和魏布尔模数m确定了幸存概率Y（值越大，临界缺陷的离散度越小）［1］

    体积为V₀试样的幸存概率Y（V₀） 取决于临界缺陷的大小和缺陷定向的分布，可用魏布尔模数m表示（图2-1-23b）。强度模数σ₀对应于37%的幸存概率同样与材料有关。魏布尔模数越大，σ0可承受的应力间隔就越短，则材料的价值越高、可靠性越好。基于线弹性断裂机理，脆性材料的抗压强度比抗拉强度高得多。由临界缺陷概率分布导致的结果可用脆性材料强度与体积的关系来表示，如方程式（2-1-6）所示：随着体积减小，可承受的应力降低。由此可以推导出纤维悖论，即材料越薄，强度越高［14］。采用这个悖论可以解释碳纤维、陶瓷纤维和玻璃纤维所具有的高强度。
    当应力幅值在弹性变形范围内时，经常被低估的还有在交变载荷作用下的材料损伤机制［1～5］。交变载荷通过应力下限σu、应力上限σo和平均应力σm来定义（图2-1-24b）。在金属材料中，即使在弹性区域内也会有（可分解的）位错运动。在交变载荷作用下，该位错运动会在滑移面产生集中。随着载荷交变周期延长，位错运动会在材料的表面生成微观缺口。首先倾向滑移面的短裂纹是从达到一定的应力强度开始的，裂纹随着每个应力强度周期而生长，直至断裂。采用对试样施加恒定应力幅值载荷的方法，可以测试出材料寿命的相关性（断裂载荷循环次数N）。测试结果采用断裂概率P（P=0表示不发生断裂）的离散宽度在沃勒线上（图2-1-24a）表示出来。在弹性变形的持久强度区域，对断裂载荷循环次数N，有Basquin关系式（2-1-7a），其中a为根据经验确定的指数。

    有些金属（如铁素体钢与β钛合金，但不是所有汽车用金属）具有非常好的疲劳强度，在某一应力幅值内不会产生疲劳损伤。对于持续交变载荷的情形，构件的设计无法充分利用材料的弹性极限能力，而是受限于材料的抗疲劳能力。
    对于高负载的韧性材料，在一定的载荷循环次数下，略微超出弹性极限是允许的。在低周疲劳循环载荷作用下的寿命，可以通过MansonCoffin法则方程式（2.1.7b）来计算，其中，Δεpl为塑性变形幅值，b为根据经验确定的指数。

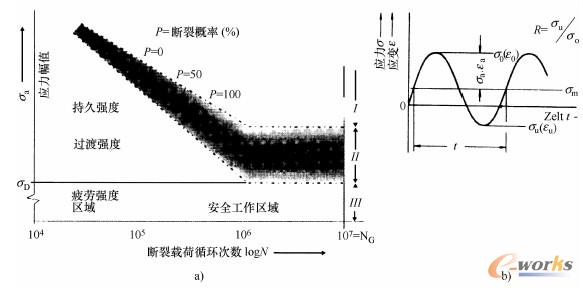
图2-1-24在周期交变载荷下的疲劳强度

a）带有针对持久强度的断裂概率以及疲劳强度区域的沃勒线

b）应力幅值在σu和σo之间，平均应力为σm［4］

2.1.7与环境相关的损伤
    构件不仅要承受机械载荷，还要承受周围环境的交变作用。图2-1-25所示为磨损体系，用来表示复杂的交变作用。两个相对运动的固体之间的力，在与相对物体的回放路径中，通过中间材料使基体产生磨损。图2-1-25a表示了作为运动累积函数的材料磨损量W与磨损速率Wr。该函数（类似于蠕变阶段）表示了进入阶段、稳定阶段和失效阶段。最重要的磨损机理为磨蚀磨损、黏着磨损、摩擦化学磨损与表面疲劳损坏［2～4］。磨蚀磨损取决于材料的相对硬度值。轻量化材料可通过采用填充剂与增强组件显著提高材料的抗磨损能力。例如，颗粒增强铝合金的抗磨损能力要高于钢的抗磨损能力［14］。在塑料和金属中植入石墨颗粒，可以减小材料的摩擦因数，从而减少磨损。对于所有的情形都要对整个体系及其交变影响进行分析。对复合材料进行适当的材料组合，可以实现可持续的减重效果。

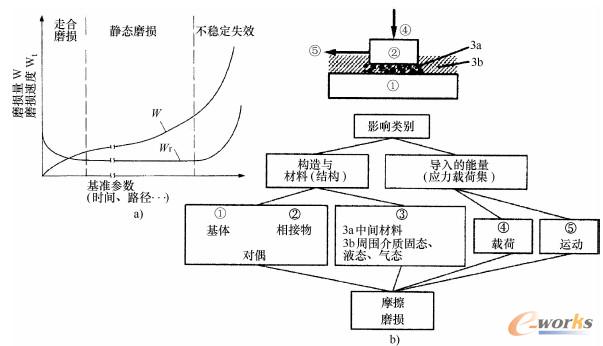
图2-1-25

a）磨损量W与磨损速率Wr，它以磨损路径为基准

（在磨损时间内均匀运动），根据b）所示的磨损体系

    随着时间的变化，腐蚀介质会减小材料的可承载横截面的面积［1～5］。对于金属来说，主要承受潮湿腐蚀。金属由正离子构成，正离子与介质的负离子亲合的倾向会导致金属大量分解。塑料容易吸收水，而氢离子会加速陶瓷和高强度金属的应力裂纹腐蚀，这些影响都会缩短材料的使用寿命。弹性极限越高，材料越容易产生应力裂纹腐蚀。材料往往不是由于金属磨损发生损坏，而多是由于形成裂纹发生损坏。根据方程式（2.1.5），产生裂纹损坏的原因是超出了材料的断裂韧度极限。在混合构造中，要注意电化学腐蚀。电化学腐蚀归因于元素化学标准电位中的距离。表2-1-4给出了几个例子：在材料耦合中，负元素溶解在电解液中。在这种情况下，镁与镁合金特别容易被腐蚀。对于铝和铝合金，可采用天然致密的氧化层来加以保护。不过，表面疲劳破坏总是可以破坏铝材料的保护层，使得铝在与其他电极为正的金属（除了镁之外的所有金属）和碳纤维增强塑料组合时都会受到腐蚀。通过在组织间隙中植入氧，可以使钛材料具有特别好的抗腐蚀能力。在温度大约为350℃以上时，这些组织间隙元素扩散速度很高，以至于会发生扩散控制的干燥腐蚀。只要在金属或者陶瓷中，氧的扩散是明显的，就要注意到这一腐蚀机理。
    如同蠕变变形一样，腐蚀作用与时间有关，在加速测试中只能给予近似评估。

2.1.8小结与展望
    材料的载荷极限构成了满足定义要求的构件设计与材料选择的基础。对轻量化来说，重量的关系意义重大。图2126中给出了高强钢（Re=1100MPa）、结构钢（S325）、铝变形合金与玻璃纤维增强塑料（GFK）等材料的载荷极限除以密度的结果示意图（不考虑周围环境的影响和热活化）：弹性极限（02%应变极限，亦即屈服强度）、106次周期下的疲劳强度与持久强度（虚线）、静态与动态断裂韧度极限。在这个极限值以下，材料可以持久承受弹性载荷。钢在室温下表现出了相对高的断裂韧度。玻璃纤维增强塑料与高强度铝变形合金的静态强度接近高强钢的静态强度，但是二者的疲劳强度则明显低于高强钢的疲劳强度。

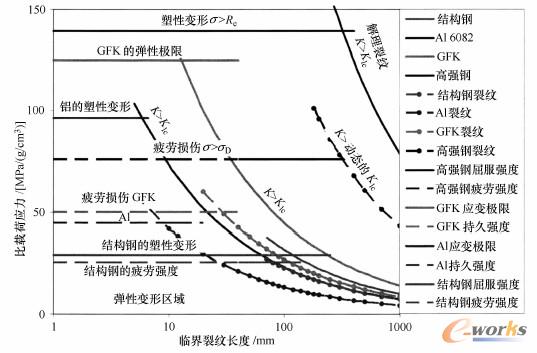
图2-1-26高强钢（HF钢）、结构钢（S235）、铝合金（A6082）、玻璃纤维增强塑料（GFK） 的材料比载荷极限的比较（以密度为基准），由在静态和动态载荷作用下与相应临界裂纹长度相关的弹性极限（应变极限或者屈服强度）、疲劳强度（持久强度与疲劳强度）、线弹性断裂韧度确定 

    但是，材料的竞争并不局限于性能，更重要的是要考虑到制造方法：板材加工、热成形或者铸造技术。成形方法和连接技术对性能也有影响。利用形状因子可以改进结构形式，材料的性价比则是经济规模生产应用的关键。23节将对这些因素进行探讨，以对材料的选择系统化。在构件开发中，要求有一个互动的过程，需要考虑到图2-1-27中所示的方方面面，最好是逐步地、以市场为标准地进行。

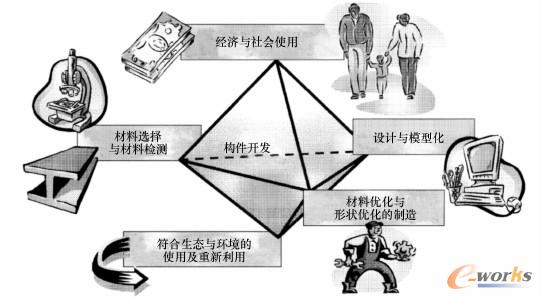
图2-1-27对材料使用性能的评估，考虑到材料重要的结构特征值、成形方法、回收

性能、经济利用价值，以及在材料使用中考虑到材料针对市场导向产品的整体适合程度参考文献