第二章 第2章 车辆简化模型及振动

      当一个实际振动系统较复杂时，建立的模型越复杂，越接近实际情况，也越能进行逼真的模拟，但往往使分析困难；建立的模型越简单，分析越容易，但得到的结果可能不精确。因此，在建立振动系统力学模型时，总是在求得简化表达和逼真模拟二者之间的折中。但一个完整系统的力学模型不仅与实际机械的结构有关，还与所研究的内容有关。以汽车这样一个复杂的振动系统为例，必须要根据所分析的问题进行简化。
1. 整车七自由度模型
      图2-1为一个把汽车车身质量看作为刚体的立体模型。汽车的簧上(车身)质量为m₂，它由车身、车架及其上的零部件总成组成，通过减振器和悬架弹簧与车轴、车轮相连接。车轮和车轴构成的簧下(车轮)质量为m₁。车轮再经过具有一定弹性和阻尼的轮胎支承在不平路面上。这个模型中，车身质量讨论平顺性时主要考虑垂直、俯仰、侧倾三个自由度，四个车轮质量有4个垂直自由度，共7个自由

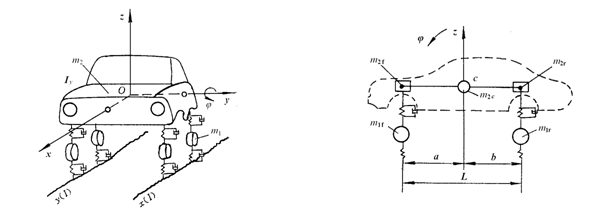
图2-1  整车7自由度模型                                                   图2-2  汽车振动系统4自由度模型

2. 双轴车四自由度模型
      当汽车对称于其纵轴线时，汽车车身只有垂直振动z和俯仰振动Φ对平顺性影响最大。这时，将汽车简化成如图2-2所示的双轴汽车4个自由度平面模型。因轮胎阻尼较小，在此予以忽略。在这个模型中，车身质量m_2c＝m_2f＋m_2r主要考虑垂直和俯仰两个自由度，前、后车轴质量m_1f，m_1r有两个垂直自由度。
3. 单轮二自由度模型
       当汽车前、后轴悬架质量分配达到一定值时，即满足以下关系

                                                                                                        

      即就是质心位置c到前后悬架的距离a和b的乘积ab，等于或接近于车身绕y轴的回转半径的平方ρ_y²，则前、后悬架系统的垂直振动几乎是独立的。因此，可以将汽车振动系统进一步简化为如图2-3所示的车身和车轮二自由度振动系统模型。图中，m₂为簧上质量；m₁为簧下质量，m₁=m_1f＋m_1r。所以，分析平顺性时，只考虑两个质量的垂直自由度。
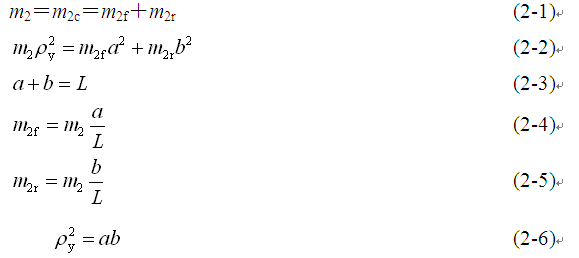
       4. 单轮单自由度模型
       在远离车轮部分，其固有频率(10Hz～16Hz)在较低激振频率范围(如5.0Hz以下)，轮胎动变形很小，忽略其弹性和轮胎质量，就得到如图2-4所示，分析车身垂直振动的最简单的单自由度振动模型。

 
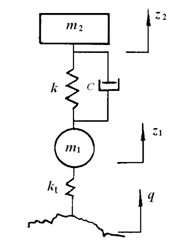
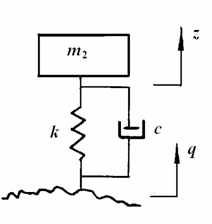
图2-3  汽车振动系统二自由度模型  图2-4  汽车振动系统单自由度模型

       5. 车身二自由度平面振动模型
       如果忽略图2-2中车轮质量和刚度，则双轴汽车平面振动模型，可简化为车身二自由度平面振动模型，如图2-5所示。

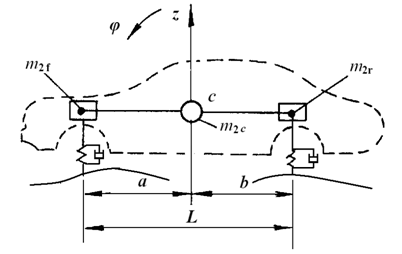
图2-5  车身二自由度平面振动模型

       尽管简化模型与实际情况有差别，但是由于实际问题非常复杂，难以进行分析研究，而通过简化模型能够为分析实际问题提供了一种简便可行的方法，且简化模型的分析结果与实际情况相差不是很大，因此，简化振动模型对于分析解决实际问题还是具有重要参考价值的。