第二章 第2章 车辆简化模型及振动
第二节 2-2 单质量车身振动及特性
2.2.1单质量车身振动微分方程
图2-6是分析车身振动的单质量系统模型,由车身质量m2和弹簧刚度k、减振器阻尼系数为c的悬架组成,q为路面激励不平度函数,它是沿路前进方向的坐标 x为参数的随机过程。
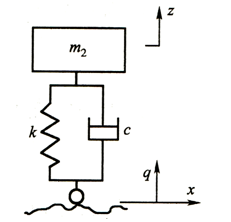
图2-6 单质量车身振动模型
取车身垂直位移坐标z的原点在静力平衡位置,可得到系统运动的微分方程为
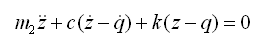 (2-7)
(2-7)
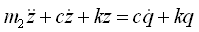 (2-8)
(2-8)
2.2.2单质量系统的自由振动响应
令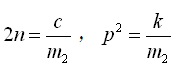 ,当激励q=0时,则由式(2-35)可得单质量系统的自由振动微分方程为
,当激励q=0时,则由式(2-35)可得单质量系统的自由振动微分方程为
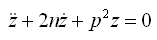 (2-9)
(2-9)
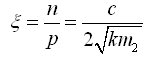 (2-10)
(2-10)
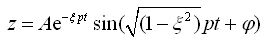 (2-11)
(2-11)
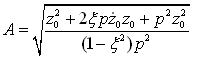 ;φ是由初始条件决定的初相角,
;φ是由初始条件决定的初相角,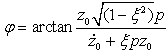 。
。由式(2-11)可知,有阻尼的自由衰减振动,车身质量m2以有阻尼的固有频率
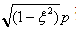 振动,而振幅却按
振动,而振幅却按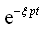 规律衰减,如图2-7所示。
规律衰减,如图2-7所示。
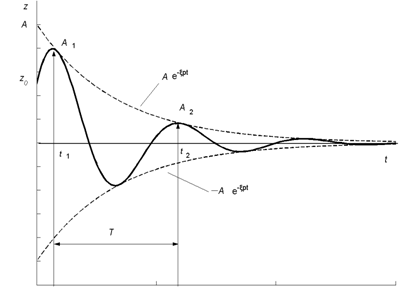
图2-7 自由衰减振动曲线
由上图2-7可知,阻尼对自由振动有两个方面的影响(1)阻尼使固有频率降低
如果无阻尼自由振动系统原固有频率
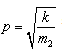 ,则弱阻尼悬架系统的固有频率p'为
,则弱阻尼悬架系统的固有频率p'为
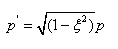 (2-12)
(2-12)
由于汽车悬架系统的阻尼比ξ在0.25左右,因此,阻尼是悬架系统的固有频率仅下降了3%左右,可以忽略不计,所以,工程上小阻尼振动系统的固有圆频率p',可以近似地认为等于无阻尼振动系统的固有圆频率p,即p≈p'。因此,车身振动的固有圆频率和固有频率,分别为
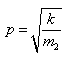 (2-13)
(2-13)
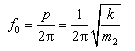 (2-14)
(2-14)
设相邻两振幅分别为Ai和Ai+1(见图2-7),它们的比值η称为减幅系数
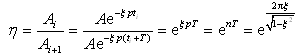 (2-15)
(2-15)
令
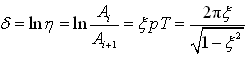 为对数衰减率,因此,可得
为对数衰减率,因此,可得
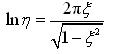 (2-16)
(2-16)
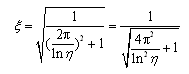 (2-17)
(2-17)
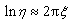 ,因此,小阻尼车辆悬架系统的阻尼比可近似表示为
,因此,小阻尼车辆悬架系统的阻尼比可近似表示为
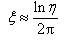 (2-18)
(2-18)
2.2.3单质量系统在简谐激振力下的响应
由于阻尼会使自由振动逐渐衰减,最后达到完全停止。工程上大都是一些能持续下去的振动必定有外加能源,弥补阻尼所消耗的能量,使系统的振动不会衰减。因此,工程上只是关系强迫振动的响应。若简谐激振力
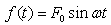 ,则根据牛顿第二定律,可得单质量振动系统在简谐激振力
,则根据牛顿第二定律,可得单质量振动系统在简谐激振力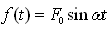 作用的振动微分方程式(2-8)可表示为
作用的振动微分方程式(2-8)可表示为
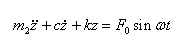 (2-19)
(2-19)
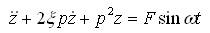 (2-20)
(2-20)
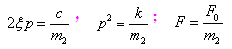
振动微分方程式(2-20)的解包括两部分:齐次方程的通解Z1和方程的特解Z2,即
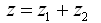
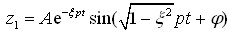 (2-21)
(2-21)
振动微分方程式(2-20)的特解Z2,代表系统在简谐激振下所产生的强迫振动,它是一种持续的等幅振动,故为稳态振动。设特解Z2为
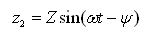 (2-22)
(2-22)
又因为
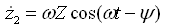 (2-23)
(2-23)
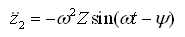 (2-24)
(2-24)
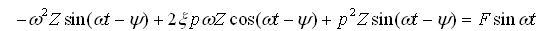 (2-25)
(2-25)
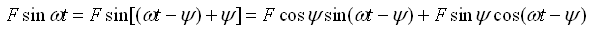 (2-26)
(2-26)
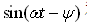 和
和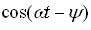 前的系数必须分别相等,即
前的系数必须分别相等,即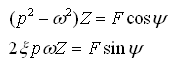
因此,可得
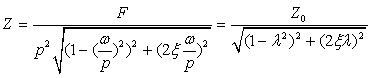 (2-27)
(2-27)
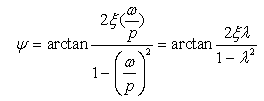 (2-28)
(2-28)
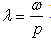 为频率比;
为频率比;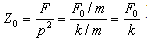 为系统的最大静位移。
为系统的最大静位移。因此,强迫振动的稳态解为
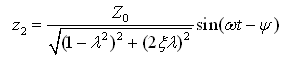 (2-29)
(2-29)由上述强迫振动解可见:在简谐激振力作用下,强迫振动响应为也简谐振动,其频率与激振频率ω相同,但相位角滞后Ψ,这是由于阻尼存在的关系。振幅Z与相位差Ψ都只与系统固有特性及激振力的性质有关,而与初始条件无关。
由式(2-27)可得,Z与Z0之比β,称为放大因子,即
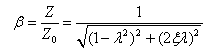 (2-30)
(2-30)
在不同的阻尼比ξ值情况下,放大因子β与频率比λ的关系以及相角Ψ与λ的关系,如图2-8和图2-9所示。其中,图2-8称为幅频响应曲线,而图2-9称为相频响应曲线。
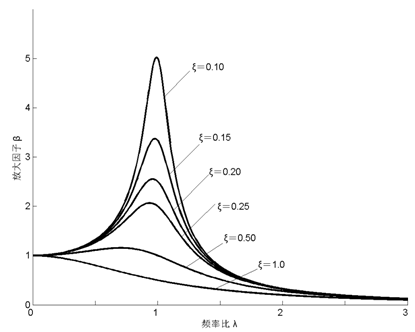
图2-8 幅频响应曲线
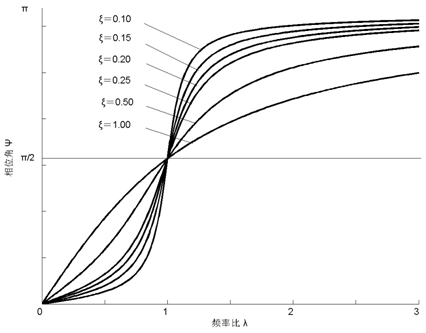
图2-9 相频响应曲线
由图2-8和图2-9可知:(1)当λ<<1,即激振频率ω远小于系统的固有频率p时,无论阻尼大小如何,β接近于1,即振幅近似等于激振力幅值F0作用下的静变形X0。故在低频区内,振幅X主要由弹簧刚度控制。此时,相位差Ψ≈0,即位移与激振力接近于同相位。
(2)当λ>>1,即激振频率ω远大于系统的固有频率p时,β趋近于0。因为激振力方向改变太快,振动物体由于惯性来不及跟随,几乎停止不动。故在高频区内,振幅X主要决定于系统的惯性。这一特性正是隔振和惯性传感器的理论依据。相位差Ψ≈π,即在高频范围内位移与激振力接近于反相位。
(3)当λ≈1时,即ω接近p,振幅X急剧增加,β趋向βmax,这种现象称为共振。严格地讲,βmax发生在
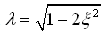 处,但通常ξ2<<1,故ω=p时系统发生共振。由式(2-27)可以看出,振幅Z达到最大值
处,但通常ξ2<<1,故ω=p时系统发生共振。由式(2-27)可以看出,振幅Z达到最大值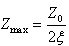 时,由式(2-28)得
时,由式(2-28)得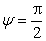 。
。可见在共振时,振幅最大值Ζmax与阻尼比ξ的值有关,ξ越小,则Ζmax将越大;在ξ→0时,Ζmax可达到无穷大。但共振时的Ψ值与阻尼比ξ的值无关,不论ξ为何值,共振时的Ψ总是π/2,这是共振时一个重要特征。从分析幅频响应与相频响应所引出的共振现象,是传统的共振试验法测定系统固有频率的理论基础。
2.2.4单质量系统在单位谐波函数激励下的响应
单位谐波函数激励为复数形式的单位幅值简谐激振力,即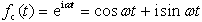 ,则单质量系统的振动微分方程为
,则单质量系统的振动微分方程为
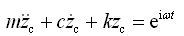 (2-31)
(2-31)
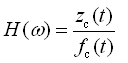 (2-32)
(2-32)
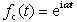 作用下所产生的振幅。对于简谐激励,若知道系统的频率响应函数,便可由式(2-32)可求得振动系统的输出响应,即
作用下所产生的振幅。对于简谐激励,若知道系统的频率响应函数,便可由式(2-32)可求得振动系统的输出响应,即
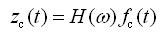 (2-33)
(2-33)
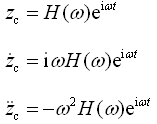
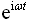 ,即得频率响应函数为
,即得频率响应函数为
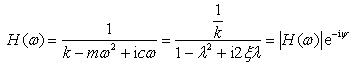 (2-34)
(2-34)
频率响应函数的模为
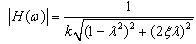 ,称为幅频特性。
,称为幅频特性。频率响应函数的相位差角为
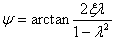 ,称为相频特性。
,称为相频特性。将复数形式的简谐激振力
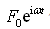 代入式(2-33),则复数形式的响应为
代入式(2-33),则复数形式的响应为
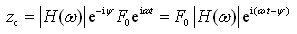 (2-35)
(2-35)
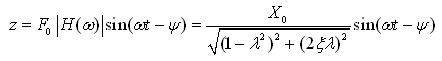
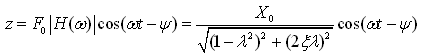
2.2.5单质量系统振动响应的付氏积分法
激励函数f(t)的傅氏积分形式为
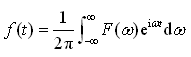 (2-36)
(2-36)
式中, 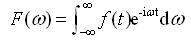 (2-37)
(2-37)
通常响应函数z(t),它可以用傅氏积分式(2-36)表示为
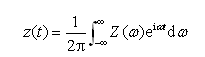 (2-38)
(2-38)
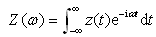 ,Ζ(ω)是响应z(t)的傅氏变换。
,Ζ(ω)是响应z(t)的傅氏变换。可以把非周期函数看成是由无数个复振幅为
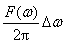 的谐波分量所组成,于是,根据式(2-35)求出对应于每个谐波分量的响应后,再根据线性系统的叠加原理,就可求得系统的响应
的谐波分量所组成,于是,根据式(2-35)求出对应于每个谐波分量的响应后,再根据线性系统的叠加原理,就可求得系统的响应
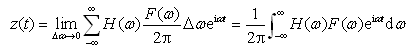 (2-39)
(2-39)
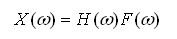 (2-40)
(2-40)
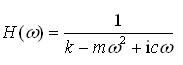 (2-41)
(2-41)
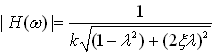 ,它的虚部与实部之比为相位角
,它的虚部与实部之比为相位角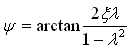 ,分别确定系统的幅频特性和相频特性,能全面反映系统的传递特性。
,分别确定系统的幅频特性和相频特性,能全面反映系统的传递特性。2.2.6单质量车身在路面激励下的振动响应
对式(2-8)通常关心其稳态随机响应,它取决于路面不平度函数随机激励q(χ)和系统的频率响应特性函数Η(ω)。由上可知,系统频率响应函数Η(ω)z~q为系统的振动响应Ζ的付氏变换与激励q的傅氏变换之比,即
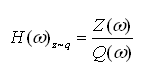 (2-42)
(2-42)
对式(2-8)进行付氏变换,可得单质量车身在路面激励下响应的频响函数为
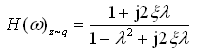 (2-43)
(2-43)
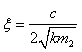 为阻尼比;λ为频率比,λ﹦ω/ρ;ω为路面激励的圆频率;
为阻尼比;λ为频率比,λ﹦ω/ρ;ω为路面激励的圆频率;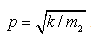 为系统固有圆频率。
为系统固有圆频率。由式(2-43)得为单质量车身在路面激励下的幅频特性和相频特性,分别为
幅频特性为
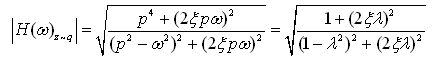 (2-44)
(2-44)
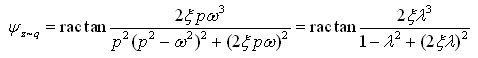 (2-45)
(2-45)
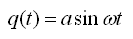
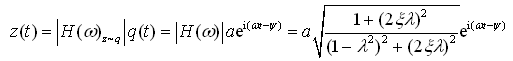
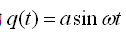 为正弦,所以系统的实际响应为
为正弦,所以系统的实际响应为
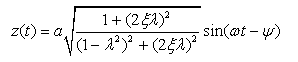 (2-46)
(2-46)
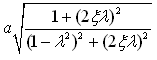 为幅值Z,即路面激励的幅值为
为幅值Z,即路面激励的幅值为
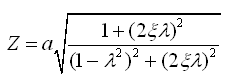 (2-47)
(2-47)
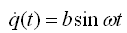 来表达,用上面同样的推导方法可得
来表达,用上面同样的推导方法可得
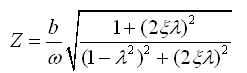 (2-48)
(2-48)
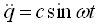 来表达,则
来表达,则
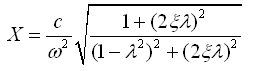 (2-49)
(2-49)
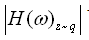 可以得到单质量系统的幅频特性曲线,如图2-10所示。
可以得到单质量系统的幅频特性曲线,如图2-10所示。
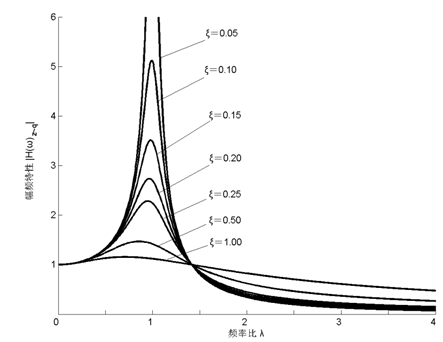
图2-10 单质量系统的幅频特性曲线
由幅频特性频响函数式(2-44)和图2-10可知(1)当频率比λ=1时,系统出现共振,幅频特性达到最大,即共振时的幅值,
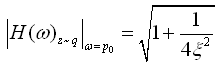
(3)共振段(0.75≤λ≤√2), |Η(ω)z~q|出现峰值,将输入激励放大,增大阻尼比ξ,可使共振峰值明显降低;
(4)高频段(λ≥√2),其中,当λ=√2时,|Η(ω)z~q|=1,系统响应与阻尼比ξ无关;当λ>√2时, |Η(ω)z~q|<1,对输入位移有衰减作用,且阻尼比减小对减振有利。