第二章 第2章 轮胎力学

      正如第2.2节所展开的内容，我们将轮胎产生侧向力和力矩的特性定义为侧偏特性。本节中，我们将更为详细地考察轮胎的侧偏特性。

231Fiala理论

      有关轮胎侧滑产生侧向力的分析中，Fiala所提出的数学模型被广为接受^［1］，通常称其为关于轮胎侧偏特性的Fiala理论，并已成为许多人用以说明轮胎侧偏特性的基础理论之一^［2］。

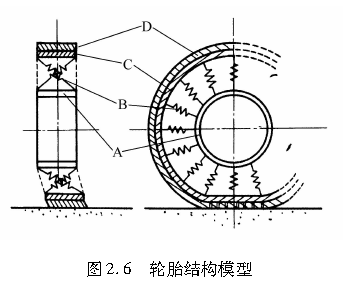
      图2.6轮胎结构模型我们将根据Fiala理论，对轮胎侧偏特性进行理论研究。轮胎的结构模型如图26所示，其中A为一个刚体，相当于车轮的轮辋；B为众多的等效弹簧，分别在径向及侧向等效替代可弹性变形的充气内胎和轮胎侧壁；C相当于较薄的轮胎胎面基底，并连接轮胎两边的侧壁；D相当于轮胎胎面橡胶，但它不是环状的连续体，而是由大量环绕轮胎圆周的独立弹性体组成的。

      当侧向力作用于轮胎接地区时，轮胎将发生侧向变形。由于轮辋是刚体，不发生变形，而轮胎胎面基底则会产生侧向的弯曲变形。因而胎面橡胶会由于胎面基底与地面之间的剪切力而发生变形，如图2.7所示

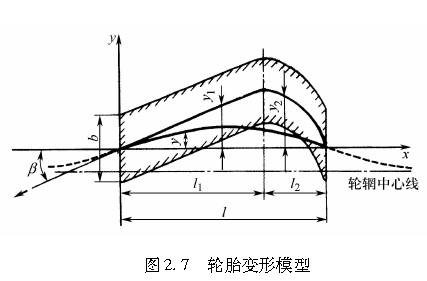
      假设在接地区的前端和后端，轮胎胎面基底的变形相等，这些点的连接线就是轮胎胎面基底的中心线，我们将其定义为ｘ轴。我们定义接地区前端垂直于ｘ方向的轴为ｙ轴。ｘ轴平行于轮辋中心线，且变形前平行于轮胎胎面基底中心线。在此坐标系下，ｘ表示沿着ｘ轴方向到轮胎接地区前端的距离，ｙ表示轮胎胎面基底偏离ｘ轴的侧向位移。ｙ_１表示在０≤ｘ≤ｌ_１范围内接地区中心线偏离ｘ轴的侧向位移，ｙ_２表示在ｌ_１≤ｘ≤ｌ范围内接地区中心线偏离ｘ轴的侧向位移。如第222小节所述，在０≤ｘ≤ｌ_１范围内,轮胎与地面间不存在相对滑动。ｌ_１≤ｘ≤ｌ则表示产生相对滑动的区域。β为轮胎的侧偏角，ｌ为接地区的长度，ｂ为接地区的宽度。

      首先，我们来观察轮胎胎面基底的侧向变形ｙ。如果轮胎胎面基底沿周向展开，则如图2.8所示，可将其视为一根无限长的梁，且该梁被放置于由众多与图2.6中的弹簧B相当的弹性基础上。
 

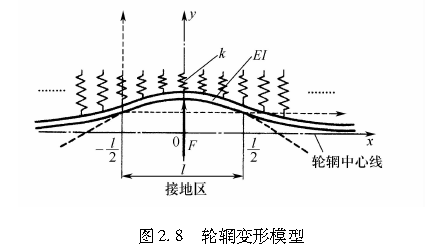
设轮胎所受的侧向力为F，取轮辋中心线为x轴，通过轮胎中心且与x轴垂直的方向为y轴，我们来考察上述梁的变形。如果轮胎所受的侧向力仅沿y方向集中作用于x=0处，可得到以下方程：

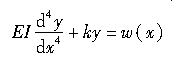（2.1）
（如果ｘ≠０，则ｗ（ｘ）＝０；如果ｘ＝０，则ｗ（ｘ）＝Ｆ）
 

式中，Ｅ为轮胎胎面材料的弹性模量；Ｉ为轮胎胎面基底的截面惯性矩；ｋ为单位长度弹性基础的弹簧常数。

对上式求解，得到侧向位移ｙ的公式为

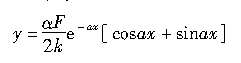（2.2）
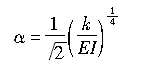（2.3）

在|ａx|＜＜1的情况下，假设接地区域内轮胎胎面基底的变形为ｙ，则有：ｃｏｓａｘ≈１、ｓｉｎａｘ≈ａｘ，于是ｙ可用ｘ的二次式近似表示如下：

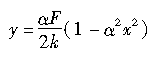（2.4）
 

此外，若移动原点使得ｙ在ｘ＝０、ｘ＝ｌ时为0，则在以该变换后的坐标下表达y如下：

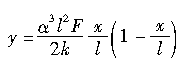（2.5）

上述方程描述了图2.7中的轮胎胎面基底侧向位移ｙ_o接下来，我们考察接地区中心线的侧向位移ｙ_２o在０≤ｘ≤ｌ_１范围内，轮胎与地面之间不存在相对滑动。接地区沿轮胎侧向行驶的反方向发生相对变形。各点沿纵向的接地面侧向位移可表示

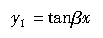（2.6）
 

轮胎胎面基底的侧向位移由式（2.5）给出，轮胎胎面橡胶的侧向位移由式（2.6）给出。如图2.9所示，胎面橡胶与胎面基底之间产生了一个（ｙ_１－ｙ）／ｄ的剪切变形。在接地区纵向的各点处，每单位长度作用有下式所示的侧向力：

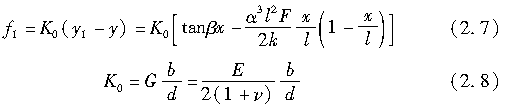
式中，G为轮胎胎面的剪切模量，ν为泊松比。

 

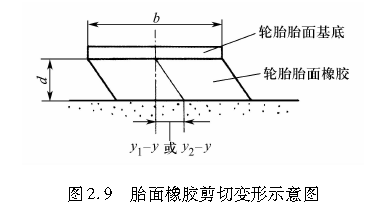
由图2.7可以看出，随着接地区向后移动，ｙ_１－ｙ将变大。如果ｆ_１的值超过地面与轮胎胎面橡胶之间的摩擦力，这两者之间将产生相对滑动，其范围为ｌ_１≤ｘ≤ｌ，且在此区域内轮胎胎面橡胶的剪切变形为（ｙ_２－ｙ）／ｄ。导致这一变形的力ｆ_２即为轮胎胎面橡胶与地面之间的摩擦力。为简单起见，设轮胎的垂直载荷为Ｗ，并假定由此载荷产生的接地区接地压力ｐ沿ｘ轴向的分布如图2.10所示，

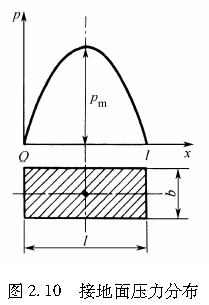
则可由峰值位于轮胎接地区中心的二次式近似表示如下：

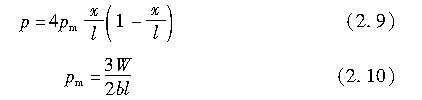
那么ｆ_２可写为

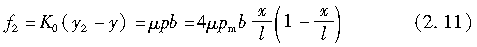
式中，μ为地面与轮胎胎面橡胶之间的摩擦系数；ｌ_１为满足ｆ_１＝ｆ_２时ｘ的值。

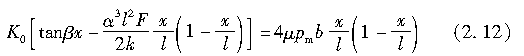
因此，通过求解上述关于ｘ的方程，得ｌ_１如下：

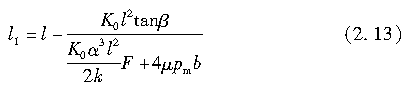
由此可得，在接地区的纵向各点处，作用于微小长度ｄ_ｘ的侧向力在０≤ｘ≤ｌ_１范围内为ｆ_１ｄ_ｘ；在ｌ_１≤ｘ≤ｌ的范围内为ｆ_２ｄ_ｘ。于是，作用于整个接地区的合力F（即侧向力）可由以下方程求得：

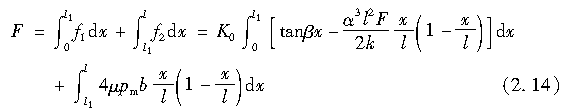
将式（2.13）代入式（2.14），并对其进行积分，则可求得两边含有F、且求解复杂的方程。于是，Fiala对此进行了近似求解如下：

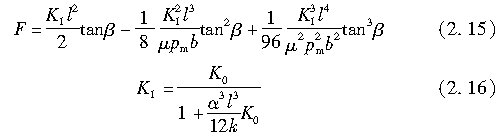
以上介绍的即为表达轮胎侧偏角与侧向力关系的基本方法。
由图2.7可以看出，作用于轮胎接地面的侧向力并非对称于接地面中心。于是，它导致侧向力产生一个绕接地面中心的铅垂轴的力矩，也就是回正力矩。作用于接地面各点处微小长度ｄ_ｘ上的侧向力所产生的绕接地区中心的力矩，在０≤ｘ≤ｌ_１范围内为（ｘ－ｌ／２）ｆ_１ｄ_ｘ；在ｌ_１≤ｘ≤ｌ的范围内为（ｘ－ｌ／２）ｆ_２ｄ_ｘ。因此，回正力矩Ｍ为

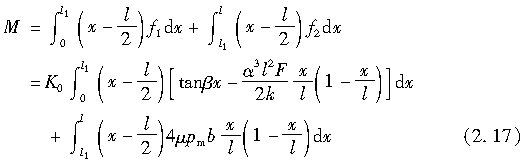
若将式（2.17）中的ｌ１用式（2.13）替换，则会使方程变得太复杂。根据Ｆ的近似式（2.15），Fiala近似求得Ｍ为

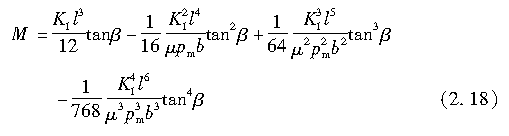
上式为表示轮胎侧偏角与回正力矩之间关系的基本方程。
当β很小时，单位侧偏角的侧向力（即侧偏刚度）表示如下：

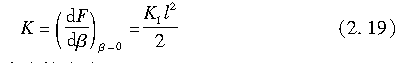
由式（2.10），轮胎的最大摩擦力为

若定义ψ为

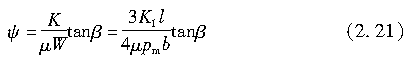
则式（2.15）和式（2.18）可写为

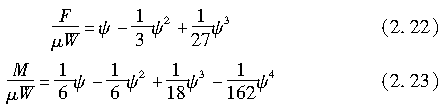
关于ψ对式（2.22）和式（2.23）进行微分，并令其为0，则可求得Ｆ／（μＷ）在ψ＝３时取最大值，为Ｆ／（μＷ）＝１；Ｍ／（μＷ）在ψ＝３／４时取最大值，为Ｍ／（μＷ）＝２７／５１２。
换言之，侧向力F在侧偏角为

时为最大，其最大值Ｆ_max为

同时，回正力矩M在侧偏角为

时为最大，最大值Ｍ_max为

根据式（2.22）和式（2.23），可绘出无量纲的侧向力Ｆ／（μＷ）、回正力矩Ｍ／（lμＷ）和侧偏角ψ＝Ｋｔａｎβ／（μＷ）的关系，如图2.11和图2.12所示。
 

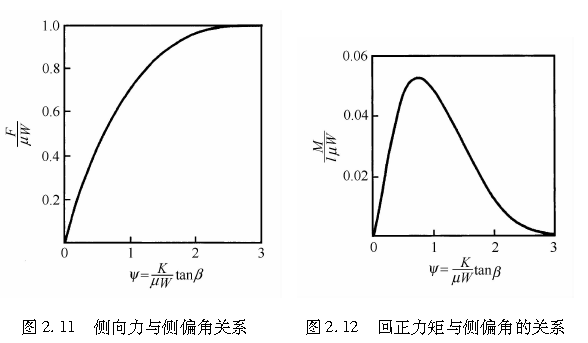
由图2.11中可以看出，当侧偏角β较小时，侧向力几乎与ｔａｎβ成正比。而当β大于某一特定值后，侧向力则趋于饱和，不再随侧偏角的增大而增大。由图2.12可见，当侧偏角β较小时，回正力矩Ｍ也几乎与ｔａｎβ成正比。当β大于某一值之后，回正力矩迅速趋于饱和，并开始随着侧偏角的增大而减小。若侧偏角β很小，则ｔａｎβ≈β，可认为侧向力和回正力矩均与β成正比。当β较大时，则侧向力不再与β成正比，即具有非线性特性。
在侧偏角较小的范围内，即ｔａｎβ≈β，β的二次及以上项可忽略不计。此时，相应于侧偏角β，侧向力和回正力矩可由式（2.15）和式（2.18）分别表示如下：

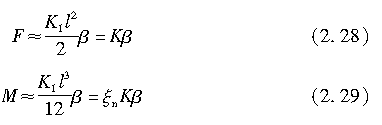
式中，K通常被称为侧偏刚度，由式（2.19）给出。根据式（2.8）和式（2.16），它可写成以下形式：

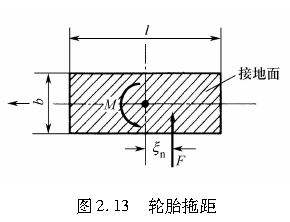
从侧向力的作用点到接地区中心的距离被称为轮胎拖距，如图2.13所示，其定义式如下：

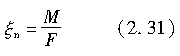
当β较小时，根据式（2.28）和式（2.29），可得其值为ｌ／６。

      到此为止，我们考察了有侧偏角时作用在轮胎上的力。接下来，我们将考察有外倾角且保持直线行驶的轮胎所受的作用力，即外倾侧向力。Fiala对有外倾角的轮胎作了如下解析。

      当考虑轮胎的外倾时，如图2.14所示，即使不产生侧偏角，轮胎胎面基底的中心线也不是直线，而是一段圆弧。

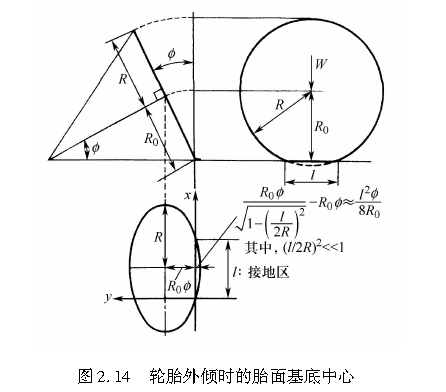
      若采用与图2.7相同的坐标系，并以抛物线近似这段圆弧，则有

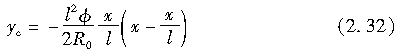
式中，Ｒ_０为轮胎胎面基底的有效半径，由下式给出：

式中，R为无载荷时轮胎胎面基底的半径；ｋ_ｅ为轮胎的纵向弹簧常数。

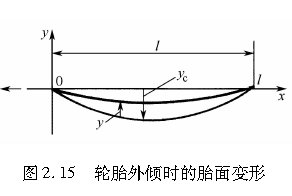
      以上情形如图2.15所示。如果轮胎在保持着外倾角的状态下自由行驶，则轮胎胎面橡胶的接地区中心将绘出如图2.5所示的弧形轨迹。然而，如果轮胎只是作直线运动，则轮胎的接地区中心应当沿着ｘ轴运动。因此，在轮胎胎面基底与地面之间的轮胎胎面橡胶上将产生剪切变形，与此变形相应的侧向力则会作用于接地区。这个力就是外倾侧向力Ｆ_ｃ。假设它集中作用于接地区中心，则由此产生的轮胎胎面基底变形为

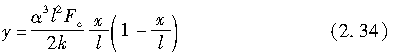
由于接地区距x轴的位移为零，故在x方向各点上的轮胎胎面基底剪切变形为：－（ｙ_ｃ＋ｙ）。因此，作用于轮胎的外倾侧向力为

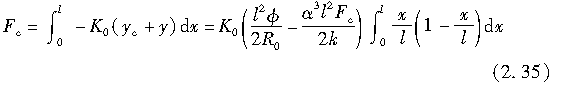
对上式积分求解，得到Ｆ_ｃ如下：

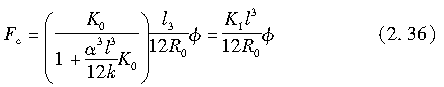
由式（2.36）可以看出，外倾侧向力与外倾角成正比，其比例系数Ｋ_ｃ被称为外倾侧向力系数。通过式（2.8），可以将它表示为

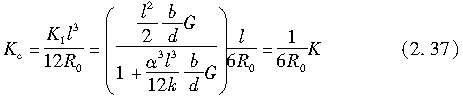
通过上述数学模型和理论分析，可得到作用于轮胎的侧向力和力矩的性质，即轮胎的侧偏特性会受到E、υ、Ｉ、ｂ、ｄ、ｋ、ｌ、μ及Ｗ的影响。

      Ｅ和υ取决于轮胎胎面的材质和构造；Ｉ、ｂ、ｄ由轮胎的形状决定；Ｗ为轮胎的垂直载荷；ｋ主要取决于轮胎的充气压力，可认为与气压成正比；ｌ主要取决于轮胎的形状，同时也受轮胎垂直载荷和轮胎充气压力的影响；μ取决于轮胎胎面的材质和路面的状态。
     
      因此，轮胎的侧偏特性主要受以下因素影响：
1）轮胎的材质、构造和形状。
2）轮胎的垂直载荷。
3）轮胎充气压力。
4）路面状态。

      理论上计算上述四种因素对之前总结的各轮胎特性参数的影响并不容易，直接通过实验测量这些影响也不简单。然而，测量具有侧偏角或者外倾角的轮胎侧向力和力矩反倒是简易可行的。因此，通常通过直接的实验结果来证实上述四种因素对于轮胎侧偏特性的影响。

例题2.1

      通过分析轮胎侧向力引起轮胎侧向变形的机理，试估计侧向力饱和时所对应的轮胎侧偏角，并验证所估计的侧偏角与式（2.24）的表达相符。

题解：位于饱和点的侧向力等于μＷ，其中μ为轮胎与路面间的摩擦系数，Ｗ为轮胎的垂直载荷。根据式（2.5），由侧向力而产生的轮胎胎面基底侧向位移可表示为

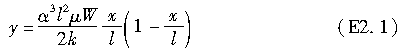
在饱和点处，沿轮胎接触印迹分布的侧向力等于轮胎垂直载荷与摩擦系数μ的乘积，即

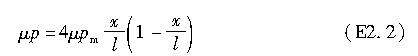
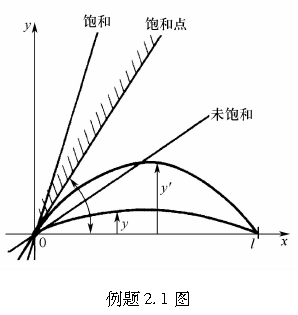
如例题2.1图所示，轮胎胎面基底的剪切变形表示为ｙ′－ｙ，其中ｙ为轮胎接触印迹的侧向变形。因此，可得如下关系式：

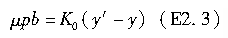
由以上三式，可求得ｙ′为：

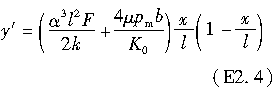
以上求得的就是轮胎接触印迹每点处侧向变形的最大值。当ｘ＝０时，ｙ′的切线方向ｄ_ｙ／ｄ_ｘ即为侧向力达到最大时对应的轮胎侧偏角。因此，轮胎侧偏角可被描述为：

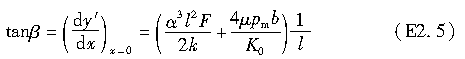
结合式（2.8）、式（2.10）、式（2.16）和式（2.19），可将上式转化为与式（2.24）相同的形式：

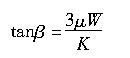
从而验证了所估计的侧偏角与式（2.24）所表达的相符。

232侧向力

本节将对给定材质和构造的轮胎，通过轮胎侧偏特性的实验验证，进一步地详细理解轮胎侧向力和力矩的特性。

1一般特性

      正如前述的理论模型所预测，当侧偏角较小时，它与侧向力几乎呈线性关系。当侧偏角超过某一值后，侧向力的增加变得缓慢，并最终在ｔａｎβ＝３μＷ／Ｋ处达到饱和。图2.16给出了一个普通的轿车用轮胎侧向力与其侧偏角之间的关系。

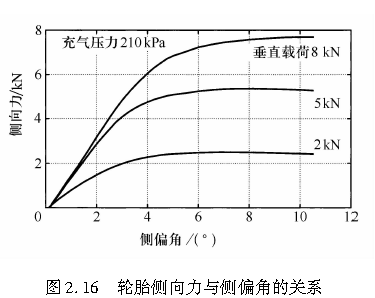
      该例中，当β小于4°左右时，侧向力是呈线性增加的。一旦超过此值，随着侧偏角的增加，其增加变得愈加缓慢，并最终在侧偏角为8°～10°时达到饱和。而对一辆普通的轿车而言，其侧向运动通常是在线性区域范围内发生的。其线性部分的斜率即对应于式（2.30）中的轮胎侧偏刚度，即单位侧偏角产生的轮胎侧向力，它是评价轮胎侧偏特性的一个重要参数。

2垂直载荷和路面条件的影响

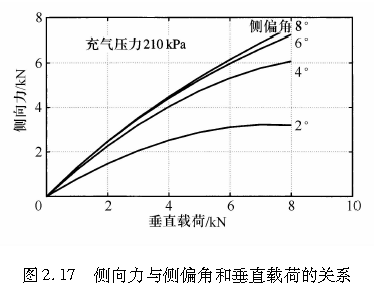
      轮胎垂直载荷对侧向力的影响如图2.16所示。当侧偏角很小时，轮胎垂直载荷对侧向力几乎没有影响。随着侧偏角的增大，侧向力的饱和值之间的差异逐渐变得显著。前面介绍的数学模型表明，只有在轮胎胎面基底与地面发生相对滑动的区域，轮胎垂直载荷才对侧向力产生影响。当接地区中产生这种相对滑动的部分较多时，即侧偏角很大时，轮胎侧向力的大小将接近于μ和Ｗ的乘积，因而垂直载荷的影响将十分明显。图2.17给出了一个轮胎垂直载荷影响轮胎侧向力的例子。

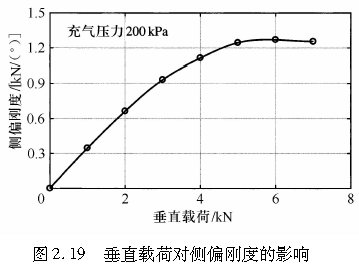
      接下来我们研究轮胎垂直载荷对轮胎侧偏刚度的影响。由图2.16可以看出，当轮胎载荷较小时，侧偏刚度随着载荷一起增加，但当载荷超出某一极限时，侧偏刚度可能会减小。

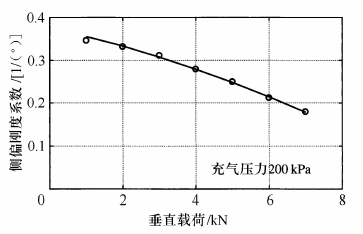
      将侧偏刚度与此时的载荷相除所得的值，称为侧偏刚度系数。如图2.18所示，侧偏刚度系数随着轮胎载荷的增大而几乎呈线性地减小。因此，侧偏刚度与轮胎载荷的关系可写为

式中，c为载荷在零附近的侧偏刚度系数，c_１为其载荷相关系数。

      轮胎侧偏刚度与轮胎载荷的关系曲线可近似为一条经过原点的抛物线。侧偏刚度先随着轮胎载荷的增大而增大至一个峰值，之后随着轮胎载荷的增大而减小。轮胎通常在侧偏刚度随载荷增加的范围内工作。

      图2.19给出了一个实际的轮胎侧偏刚度随载荷的变化关系曲线，证实了二者的关系可近似为一条抛物线。

      通常情况下，轮胎垂直载荷的影响以μＷ的形式来表述。轮胎胎面基底与路面间的摩擦系数μ的影响和垂直载荷相同。图2.20示意性地给出了随着轮胎侧偏角的变化，不同路面条件对侧向力的影响。

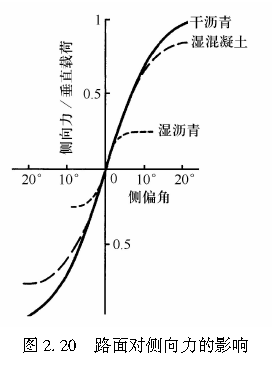
      由图2.20可见，当侧偏角较小时，摩擦系数对侧向力几乎没有影响，而当侧偏角较大时则有显著影响。可见，摩擦系数对侧向力的影响与垂直载荷的影响相似。

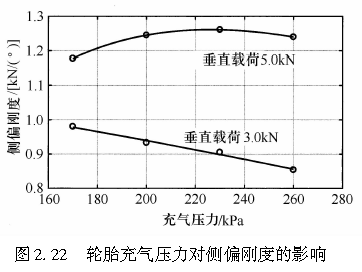
3胎压的影响

      在前面的第231小节中，通过对轮胎数学模型的分析可清楚地得知，对某恒定的力而言，轮胎胎面基底的变形ｙ越小，则轮胎的侧向力越大。由式（2.5）可知，α^３l^２／（２ｋ）的值越小，则ｙ值越大。如果弹性基础的弹簧常数ｋ以及轮胎胎面基底的弯曲刚度EI越大，则轮胎胎面基底的变形就越小。由于弹簧常数ｋ取决于轮胎充气压力，因此我们可以预测：侧偏力应该会随着轮胎充气压力的增大而增大。然而，增大轮胎充气压力会减小接地面长度ｌ，而由式（2.15）可知，侧向力会随着接地区长度的减小而减小。

      图2.21就是一个很好的例子，它表示了侧向力和轮胎充气压力之间的关系。一方面，ｋ随着轮胎充气压力的增大而增大，侧向力应该增大；而另一方面，轮胎充气压力增大导致接地区长度l减小，会使侧向力减小。最终我们发现可以一个有趣的现象，即在图中所示的充气压力变动范围内，侧向力几乎恒定不变。
 

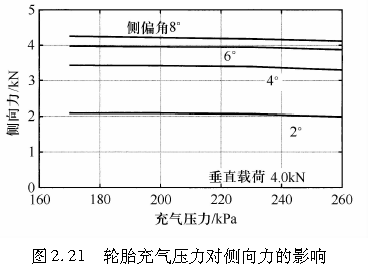
      以上观点可以通过侧偏刚度和轮胎充气压力间的关系得到进一步证实，如图2.22所示。当垂直载荷相对较小时，接地区长度对侧向力的影响比弹簧常数ｋ大，即此时的侧偏刚度随着轮胎充气压力的增大而减小；另一方面，当垂直载荷相对较大时，弹簧常数ｋ对侧向力的影响接地区长度比大，即此时的侧偏刚度随着轮胎充气压力的增大而增大。然而，对于更大的垂直载荷，轮胎充气压力增大对接地区长度的影响更大，因而侧偏刚度会随着轮胎充气压力的增大而减小。上述观点可以通过式（2.30）来理解。

4轮胎形状的影响

      轮胎胎面基底的弯曲刚度EI由轮胎的形状决定。如果给定轮胎的材质和构造，则轮胎形状产生的影响主要取决于轮胎胎面基底的转动惯量Ｉ。通常，轮胎尺寸越大，Ｉ值越大。对于半径相同的轮胎，宽度大的扁平轮胎Ｉ值较大。因此，为了获得大的侧向力，我们希望将轮胎制造成扁平形状。

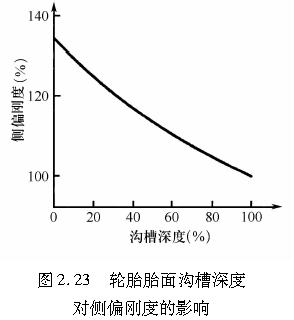
      由式（2.30）可知，当ｂ增大而ｄ减小时，轮胎侧偏刚度增大。图2.23表示与轮胎胎面橡胶厚度相当的轮胎胎面沟槽深度与侧偏刚度的关系。从图中可以看出，由于轮胎胎面磨损而使ｄ等效减小的轮胎，其侧偏刚度将变大。

5驱动力和制动力的影响

      前面已经考察了轮胎参数和垂直载荷对侧向力的影响。在制动或者驱动过程中，轮胎不仅会受到支撑车辆荷重的垂直载荷，还会在接地区处受到使车辆制动或者驱动的纵向力，后者也会影响轮胎的侧向力。
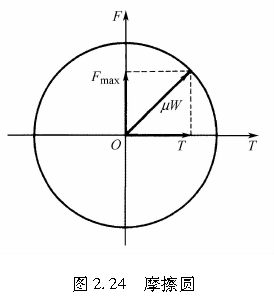
      基于经典的摩擦定律，如图2.24所示，作用于轮胎上的侧向力F和驱动力（或者制动力）T总是满足以下不等式：

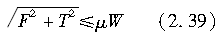
      换言之，作用于轮胎与地面接触面内的水平合力不会超出其垂直载荷与摩擦系数的乘积。这表明，合力的矢量只能位于半径为μＷ的圆内，我们称此圆为摩擦圆。

      如果轮胎在纵向受到驱动力或者制动力的作用时，则在大侧偏角下时能达到的最大侧向力为

而且若Ｔ＝０，则上式与式（2.25）相一致。
      当驱动力或者制动力为零时，侧向力Ｆ_０与侧偏角的关系由图2.25中的曲线段Ｏ---Ａ_０给出；当驱动力（或者制动力）作用时，侧向力与侧偏角的关系则由图中的曲线段Ｏ---Ａ给出。假设不论侧偏角如何，即在任何值时由驱动力（或者制动力）引起的侧向力的下降率是相同的，则有下式成立：

或者

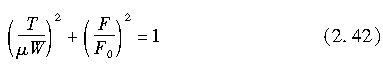
表明对给定的侧偏角而言，侧向力F与驱动力（或者制动力）T的关系曲线为一椭圆。在侧向力取最大值所对应的侧偏角处，该椭圆与之前所示的摩擦圆一致。图225表明了F与T满足椭圆关系的情形。 
 

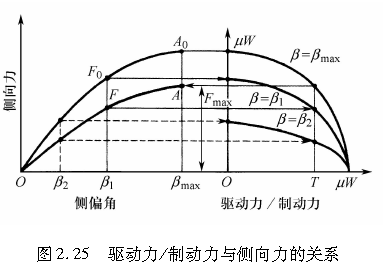
      有关驱动力和制动力对侧向力的影响，已进行了很多的研究。图2.26为一个实际测得的例子，或许可用来理解上述摩擦圆的概念。
 

233自回正力矩

      根据数学模型所进行的理论分析表明，当侧偏角较小时，回正力矩随着侧偏角线性增加；而随着侧偏角增大，回正力矩趋于饱和并达到某一特定峰值，随后便开始随着侧偏角的增大而减小。
      对一个真实的轮胎，其侧偏角与回正力矩之间关系的典型实例由图2.27给出。

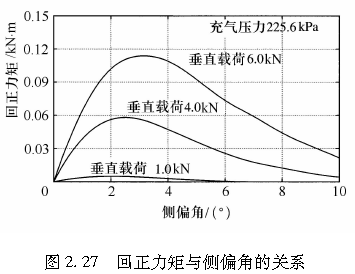
      图2.27表明了不同侧偏角情况下，轮胎垂直载荷对回正力矩的影响。当侧偏角较小时，轮胎垂直载荷对侧向力的影响较小，而在侧偏角较大的情况下影响较明显。与此相对的是，不论侧偏角如何，轮胎垂直载荷对回正力矩的影响都很大。一个原因就是，垂直载荷的影响发生在轮胎接地区与胎面橡胶之间存在相对滑动的范围内，而回正力矩本身也特别受作用于接地区前、后两端的侧向力的影响。另一个原因是，轮胎垂直载荷的增大会导致接地区长度的增大，从而使得由侧向力产生的力矩也随之增加。这点或许可以由式（2.18）得到验证，我们看到其中包含有l的三次项或更高次项。

      如果增大轮胎充气压力，则如前面所述，在某些情况下侧向力会增大，从而回正力矩也会增大。然而，对一个真实的轮胎而言，其回正力矩会随着轮胎充气压力的增大而减小。原因是：虽然侧向力随着轮胎充气压力的增大而增大，但与此同时，接地区长度也减小了，这会对回正力矩的大小产生很大影响。回正力矩随着轮胎充气压力的减小而增大，但若轮胎充气压力低于某个值时，回正力矩便不再增大了。原因是如果轮胎充气压力太小时，侧向力的减小对回正力矩的影响更明显。

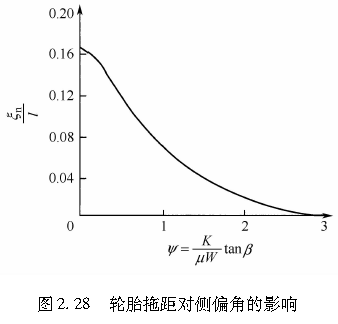
      回正力矩是侧向力绕过接地点中心的铅垂轴的力矩。轮胎拖距的定义如图2.13所示。利用式（2.22）和式（2.23），可得到图2.28所示的ξｎ＝Ｍ／Ｆ与ψ之间的关系。由图可见，一旦侧偏角增大，ξｎ的值就会急剧减小。

 234外倾侧向力

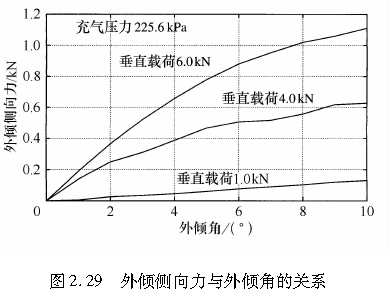
      由式（2.36）可知，当侧偏角为零时，轮胎的外倾侧向力与外倾角成正比。图2.29给出了一个普通轮胎外倾角与外倾侧向力之间关系的实例。该实例表明，外倾侧向力与外倾角成正比。此外，该图还表明了轮胎垂直载荷对外倾侧向力的影响。从图中可以看出，外倾侧向力系数（即单位外倾角对应的外倾侧向力）几乎随着轮胎垂直载荷呈线性增大。如图2.14所示，轮胎胎面基底的有效半径Ｒ_０与轮胎垂直载荷Ｗ有关，其关系由式（2.33）确定。接地区长度也随轮胎载荷的增大而增大。由式（2.37）可知，外倾侧向力系数取决于垂直载荷，并随着垂直载荷的增大而增大。该式还可得出，外倾侧向力系数等于侧偏刚度与ｌ／６Ｒ_０的乘积。那么，我们就可以假定外倾侧向力系数与侧偏刚度具有相似的特性。由于轮胎接地区长度ｌ和有效半径Ｒ_０的比值ｌ／Ｒ_０通常在0.3左右，因此外倾侧向力系数通常小于侧偏刚度的十分之一。
 

      至此，我们考察了由侧偏角引起的外倾侧向力和侧向力。但普通车辆的轮胎在行驶中通常是同时有侧偏角和外倾角的。在这种情况下，侧向力和外倾侧向力可看成是各自独立作用的。

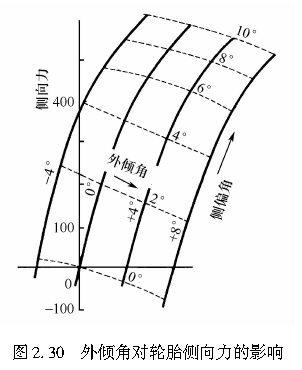
      图2.30是Ellis^［２］提出的侧偏角和外倾角共同作用产生侧向力的一个例子。图中的曲线表明了不同侧偏角情况下，外倾角与侧向力的关系；同时表明不同外倾角下，侧偏角与侧向力的关系曲线分别互相平行。以上表明，由外倾角和侧偏角产生的作用于轮胎上的侧向力可各自、独立地进行处理。

      近年来，特别在轿车上，通常使用扁平轮胎。当发生外倾时，扁平轮胎接地区内轮胎载荷的侧向分布很容易形成内侧轮胎载荷大而外侧载荷小的不均匀分布。在此不均匀分布的情况下，轮胎所产生的侧向力要小于均匀分布的情况。这点也可以从以下事实推测而得：侧向力和侧偏刚度对载荷的相关性如图2.17和图2.19中的抛物线所示，由图可见，由轮胎载荷减小引起的侧向力的下降，比由轮胎载荷增大而引起侧向力的上升更多。

      因此，即使通过加入外倾角使得由侧偏角引起的外倾侧向力和侧向力是同一方向的，但由于外倾角会引起轮胎载荷分布发生变化，从而会进一步导致侧向力的减小，因而由侧偏角和外倾角引起的总侧向力也会减小。

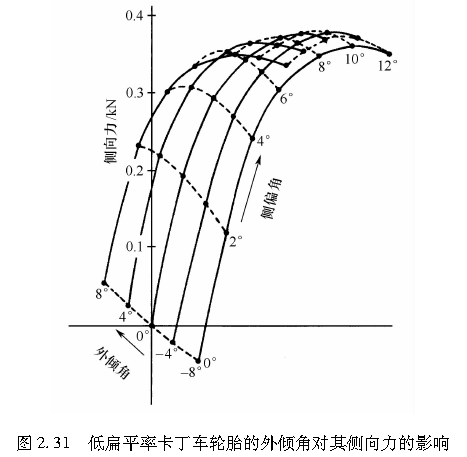
      为了全面地理解上述现象，图2.31给出了一个卡丁车扁平轮胎的研究结果来加以说明。