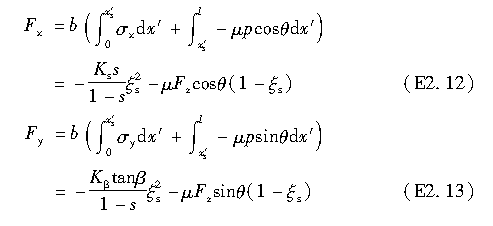第二章 第2章 轮胎力学

241数学模型

      第231小节中，我们已根据Fiala理论解释了轮胎的侧偏特性。所采用的数学模型假设：伴随着轮胎侧向滑动，其胎面基底相对于其轮辋发生侧向弹性变形，同时胎面橡胶相对于胎面基底进一步发生侧向弹性变形。
      同样采用这个数学模型，我们可以考察纵向力（如驱动力和制动力）的影响，但模型会变得过于复杂。取而代之的是，根据图2.32表示的轮胎胎面橡胶环绕刚性轮辋的情形，我们将轮胎胎面基底作为唯一的弹性部分。这样的轮胎模型允许同时在纵向和侧向考察弹性变形。与前面的模型相似，认为这个轮胎胎面橡胶并非环状的连续体，而是由沿轮胎周向的独立的无数弹性体组成的。我们称该轮胎模型为刷子模型。

 

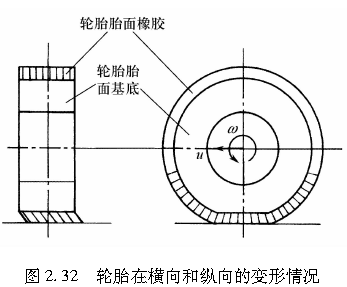
      下面我们采用这个轮胎模型，从理论上理解轮胎在纵向及侧向产生的力^［3］。

242驱动和制动情况下轮胎的侧向力

      如图2.33所示，设轮胎以角速度ω旋转，并同时沿与其回转平面成β角的方向行驶，其回转面方向的速度分量为ｕ。我们称作用于轮胎的三个力分别为纵向力Ｆ_ｘ、侧向力Ｆ_ｙ和垂向力Ｆ_ｚ。
 

 

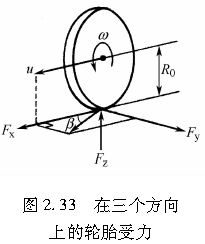
1制动情况下

      如图2.34所示，设轮胎接地区中心线的前端为坐标原点，并取纵向为ｘ轴、侧向为ｙ轴。另设Ｏ点正上方的轮胎胎面基底处的点为Ｏ′。经过时间Δｔ，接地点从Ｏ点移动到Ｐ点，轮胎胎面基底的点从Ｏ′点移动到Ｐ′点。将Ｐ′点在ｘ轴上的投影记为Ｐ″点。
     
      在Δｔ时间内，自Ｏ点进入的接地点在ｘ轴方向上前进的距离，即Ｐ点的ｘ坐标为
 

 

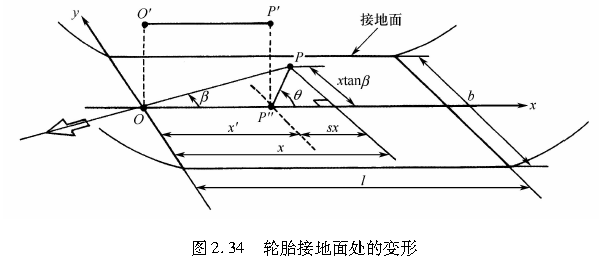
自Ｏ′点进入的点Ｐ″的ｘ坐标为

因此，P点和P′点在ｘ方向上的相对位移，即轮胎胎面橡胶的变形为

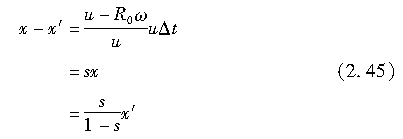
这里的s为轮胎纵向滑移率，等于：

并且自O点进入的接地点在y方向上的位移，即P点的y坐标为

由于Ｐ′点在ｙ方向上无位移，因而它就是轮胎胎面橡胶在ｙ方向上的变形。

      因此，作用于Ｐ点每单位长度在ｘ方向的力σ_ｘ和每单位宽度在ｙ方向上的力σ_ｙ分别为

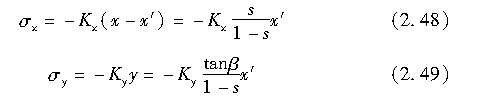
式中，力的正负号与x轴和y轴的正负方向相反。此外，二者合力的大小为

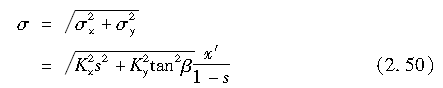
式中,Ｋ_ｘ为轮胎胎面橡胶单位长度的纵向刚度；Ｋ_ｙ为单位宽度的侧向刚度。

      当轮胎产生纵向滑移率及侧偏角后，轮胎会发生变形。结果形成与ｘ′成比例的轮胎接地区力的分布。
      设轮胎接地压力分布与第231小节中的相同，有

      如图2.35所示，在０≤ｘ′≤ｘ′_ｓ的附着区范围内，作用于轮胎接地区的力由式（2.50）表示；在ｘ′≥ｘ′_ｓ的滑移区范围内则以μｐ表示。
 

 

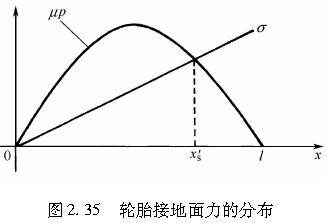
      在附着区范围内，作用于接地区x方向和y方向上的力分别为σ_ｘ和σ_ｙ；在滑移区范围内，相应的作用力则分别为μｐｃｏｓθ和μｐｓｉｎθ，这里的θ决定了轮胎侧滑的方向。
     
将σ＝μｐ代入式（2.50）和式（2.51）中，求解ｘ′_ｓ，并假设一个无量纲量ξ_ｓ为

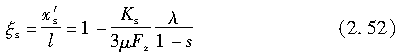
其中，

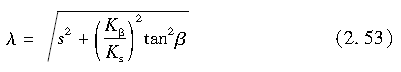
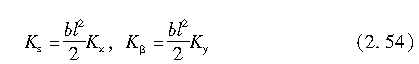
由上可知，作用于轮胎整个接地面在ｘ方向和ｙ方向上的力表述如下：
      当ξ_ｓ＞０时，对由附着区和滑移区组成的接地区，有
 

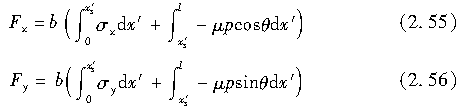
而当ξ_ｓ≤０时，即对只存在滑移区的接地面，有

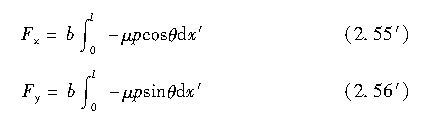
将式（2.50）～式（2.52）代入式（2.55′）～式（2.56′），可求得Ｆ_ｘ和Ｆ_ｙ如下：
当

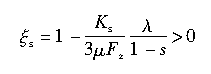
则，

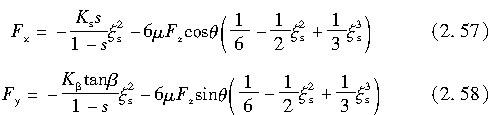
当

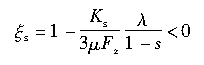
则，

这里，假定滑移力的方向θ近似为滑动起始点处的滑移方向，即

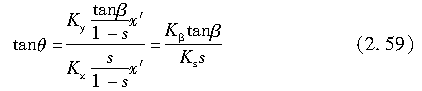
故得：

由式（2.54）定义的Ｋ_ｓ相当于在β＝０、ｓ→０时单位纵向滑移率所对应的纵向力的总和；而Ｋ_β相当于β→０、ｓ＝０时单位侧偏角对应的侧向力的总和。以上结论也可在Ｋ_ｓ和Ｋ_β很小且β＝０或ｓ＝０时，通过对接地区的作用力积分得到。式（2.57）和式（2.58）分别证实了（αＦ_ｘ／α_ｓ）_{ｓ＝０，β＝０}＝Ｋ_ｓ、（αＦ_ｙ／αβ）_{ｓ＝０，β＝０}＝Ｋ_β。因此，如果要用我们描述的模型将Ｆ_ｘ和Ｆ_ｙ用于数值模拟，一个实际的做法是，依照轮胎垂直载荷、根据实验来确定Ｋ_ｓ和Ｋ_β。

      由于摩擦系数μ是轮胎垂直载荷Ｆz和滑移速度Ｖ_ｓ的函数，因此期望有一个能反映μ对轮胎载荷和滑移速度的经验公式。这里，我们定义Ｖ_ｓ为

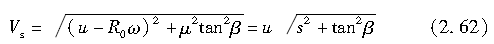
如式（2.63）所示，作为纵向滑移率s、侧偏角β、轮胎载荷Ｆz和轮胎行驶速度ｕ的函数，轮胎的纵向力和侧向力可以通过数值求解获得，即

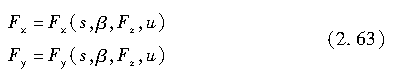
2驱动情况下

      与制动时相同，考虑轮胎胎面橡胶相对于轮胎胎面基底的变形，则有

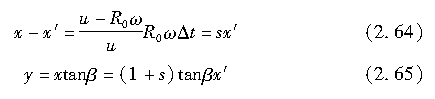
式中，ｓ为加速过程中轮胎的纵向滑动率。

故有

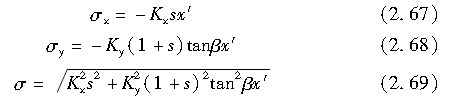
参照制动时的情况，由下述公式求出附着区和滑动区的边界点：

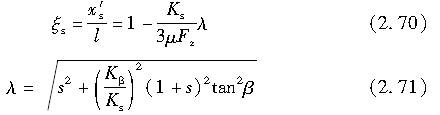
在加速情况下，推导得出在ｘ方向和ｙ方向作用于轮胎接地区的力如下：
当

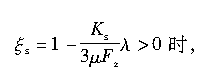
则，

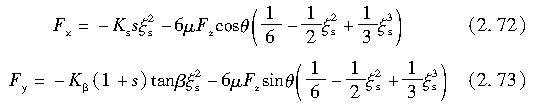
当

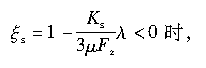
则，

其中，

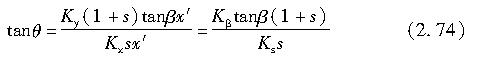
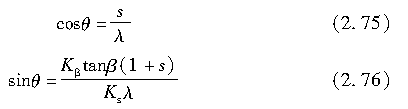
并且滑动速度为

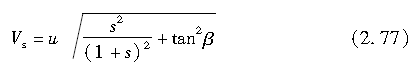
以式（2.57）～式（2.58′）及式（2.72）～式（2.73′）求得的驱动和制动时作用于侧滑轮胎的纵向力和侧向力由图2.36所示。
 

 

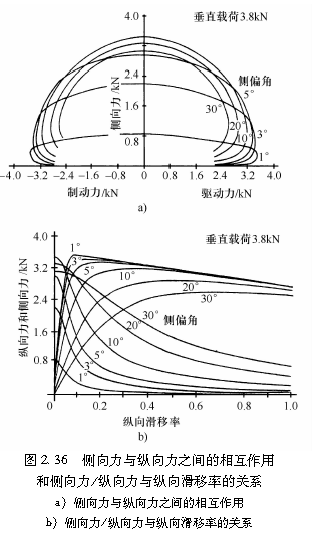
      清晰地可见，这里所进行的理论分析很好地解释了在第232小节第五部分中所述的关于驱动力和制动力对轮胎侧偏特性的影响。

243驱动和制动情况下轮胎的回正力矩

      如第231小节所述，作用于接地区的侧向力相对于接地面中心是非对称的。因此，会产生一个绕轮胎接地面中心铅垂轴的力矩。当纵向力和侧向力同时作用时，由于轮胎的侧向变形，纵向力的作用点与轮胎中心线之间将产生偏离，并产生一个由纵向力引起的一个回正力矩。这些力矩的总和即为回正力矩。

      作用于接地区某点单位宽度、单位长度的力σ_ｘ和σ_ｙ如图2.37所示。
 

 

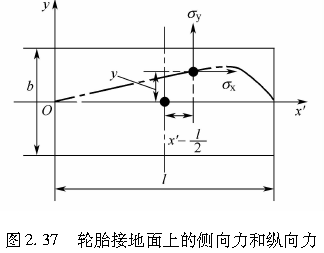
      上述的回正力矩可写成绕P点的力矩总和，即：

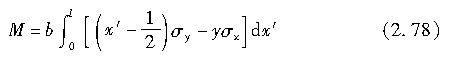
将接地区划分为附着区和滑动区，并将式（2.78）具体化，则有：

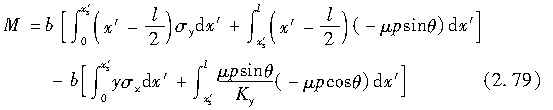
式（2.79）中的第1、2项的积分表示由侧向力引起的回正力矩，而第3、4项的积分则表示由纵向力引起的回正力矩。

      利用式（2.47）～式（2.49）或者式（2.65）、式（2.67）、式（2.68）和式（2.51），可积分求解得到回正力矩，具体如下：

      1制动情况下（ｓ＞０）



     
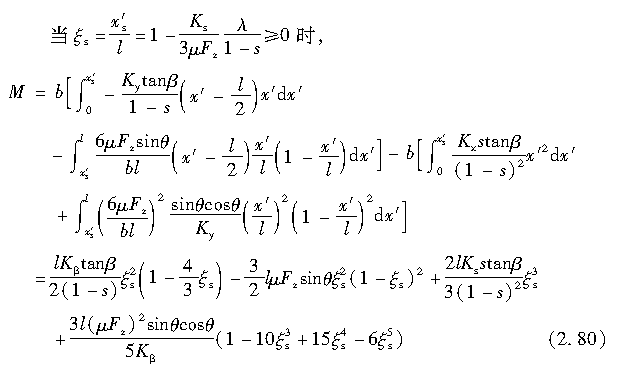
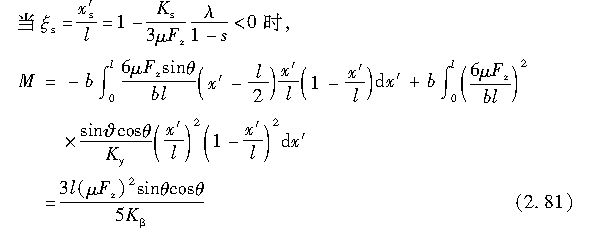
      2加速情况下（ｓ＜０）



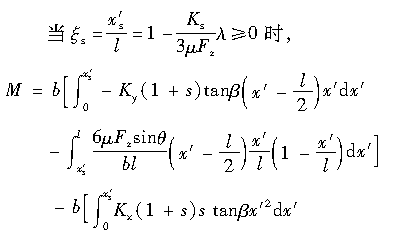
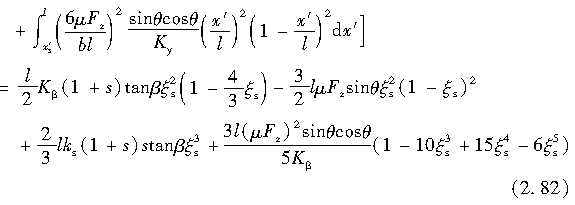
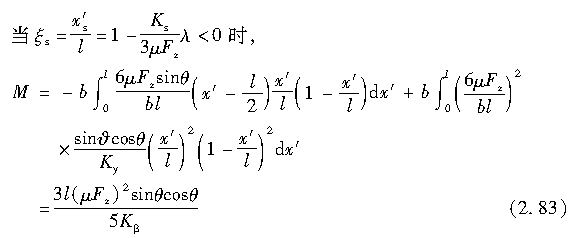
      图2.38绘出了利用式（2.80）～式（2.83）计算驱动力和制动力与回正力矩关系的结果。与轮胎侧向力的情形不同，回正力矩在驱动和制动时有很大的不同，且随驱动力或制动力以及侧偏角的变化呈现相当复杂的变化规律。
 

 

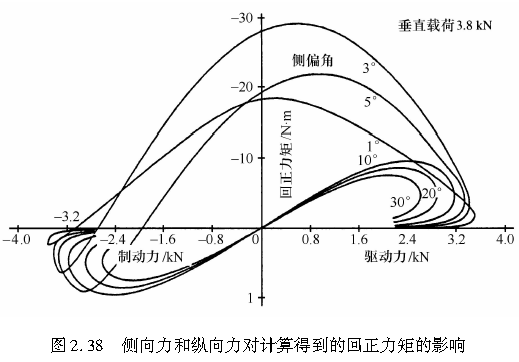
例题22

      试利用侧向力和垂直载荷分布示意图论证，对沿着纵向带有一小侧偏角的轮胎而言，由该小侧偏角引起的侧向力与侧偏角之间成比例关系。并证实，二者之间的比例关系与垂直载荷基本无关，而是取决于轮胎的侧偏刚度。

      题解：例题2.2图为小侧偏角情况下轮胎侧向力和垂直载荷的分布示意图，其中的直线表示由轮胎胎面橡胶的侧向变形而产生的侧向力，而抛物线则表示垂直载荷与摩擦系数之积的分布情况。显然由图可见，由直线和一条抛物线围成的区域表示轮胎的侧向力。当侧偏角很小时，轮胎垂直载荷的变化对其几乎没有影响；而且该区域可近似看成一个三角形，因而其面积基本与侧偏角成比例关系。由于该三角形主要取决于由轮胎胎面橡胶的侧向变形，因此由侧向变形引起的力也直接取决于轮胎的侧偏刚度。
 

 

例题23

      假如轮胎垂向接地压力在接地区上沿纵向为均匀分布，试推导出制动时轮胎的纵向力Ｆ_ｘ和侧向力Ｆ_ｙ。

      题解：由于垂向接地压力为均匀分布，则式（2.51）可变为

由于满足σ＝μｐ的ｘ′点是粘着域和滑动域的分界点，将上式和式（2.50）代入σ＝μｐ，可得如下方程：

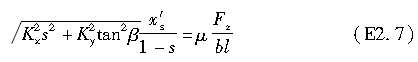
由于Ｋ_s＝ｂｌ^２Ｋ_ｘ／２，Ｋ_β＝ｂｌ^２Ｋ_ｙ／２，上式可变形为：

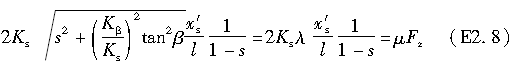
故得：

按第242小节第五部分中的处理过程，可得Ｆ_ｘ和Ｆ_ｙ如下：
当ξ_s≥１时，不存在滑动区，故有

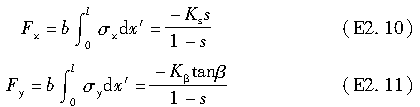
当ξ_s≤１时，同时存在附着区和滑动区，故有