第二章 第2章 轮胎力学

      到此为止，已经讨论的轮胎特性都是关于在一定的侧偏角下轮胎的侧向力和回正力矩的静态特性。而本节中，我们将考察侧偏角变化时的瞬时侧向力和回正力矩，即动态的轮胎侧偏特性。

      在第2.3节和第2.4节中，我们从理论上考察了轮胎的侧偏特性，所用的数学模型考虑了轮胎接地区部分的微小变形。但如果动态的侧偏特性也采用这些模型分析的话，就变得太复杂了。取而代之的是，我们将下面的研究仅限于小侧偏角范围，利用处理侧向变形的宏观轮胎模型考察其侧向力和回正力矩的瞬时响应。

251侧向力的动态特性

 

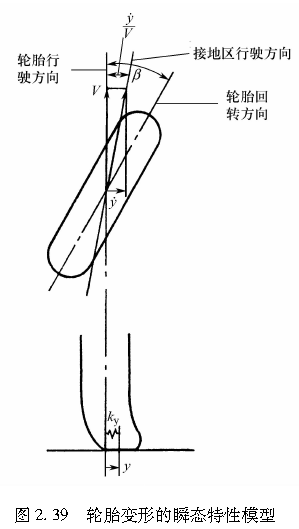
      如图2.39所示，当沿着轮胎回转方向行驶而突然产生一个侧偏角β时，在轮胎上会产生一个侧向力，并且接地面只在侧向产生大小为ｙ的变形。此时，接地区的侧向速度为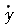，并由图2.39可知，接地区的侧偏角为。

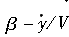      设Ｆ为轮胎的侧向力，Ｋ为侧偏刚度，则有

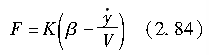
如果定义轮胎侧向刚度为ｋ_ｙ，则得：

由上两式消去ｙ，可得：

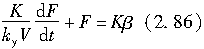
对上式进行拉普拉斯变换，并用侧向力相对于侧偏角的传递函数来表示，则有

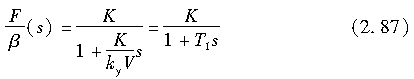
侧向力相对于侧偏角的响应可用以Ｔ_１＝Ｋ／ｋ_ｙＶ为时间常数的1阶延迟环节来近似。

      用ｊω替代式（2.87）中的ｓ，可得侧向力的频率响应如下：

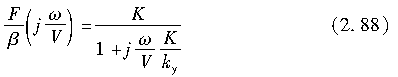
由式（2.88），侧向力相对于侧偏角的频率响应可看成是相对于距离频率，而非时间频率ω（ｒａｄ／ｓ）。图2.40即为这样的频率响应的测量实例。可见，响应可用一阶延迟环节来准确地近似表示。
 

 

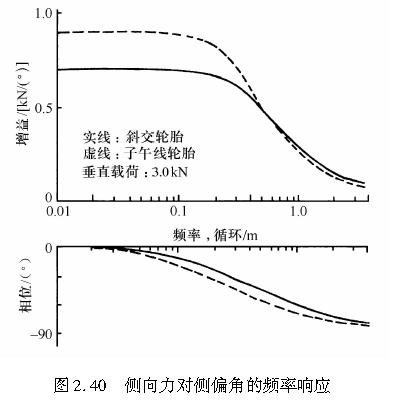
252回正力矩的动态特性

      静态的轮胎回正力矩由侧向力与轮胎拖距ξ之积给出。如第251小节所述，侧向力相对于侧偏角的瞬时响应可用一个一阶延迟环节来描述。因此，由此侧向力产生的回正力矩Ｍ_s的响应也可用一阶延迟环节来近似。设此时的时间常数为

在此情况下，当轮胎突然产生一个侧偏角时，轮胎自身将产生扭曲变形。由这种扭曲变形引起的力矩将构成瞬时轮胎回正力矩的一部分。轮胎的扭转角在侧偏角β产生的瞬间达到最大值，其大小与侧偏角一致。然而随后，扭转角会随着轮胎的转动而减小，在稳定状态变为零。因此，由轮胎的扭转而产生的力矩Ｍ_ｔ相对于侧偏角的响应可以如下的一阶延迟环节来近似表示：

式中，ｋ_ｔ为轮胎的扭转刚度。

由上可知，轮胎的回正力矩Ｍ作为Ｍ_ｓ与Ｍ_ｔ之和，可由下式表示：

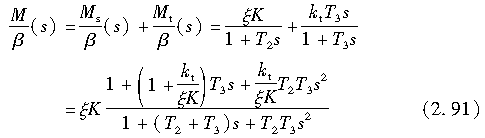
其频率响应为

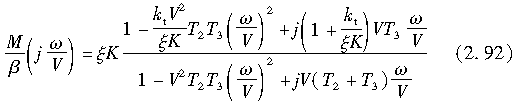
      图2.41给出了回正力矩相对于ω／Ｖ的频率响应的测量数据。图中曲线的形状证实了式（2.92）的近似结果是合理的。