第二章 轻量化的问题结构

    为了对所有轻量化措施进行经济性评估，下面来讨论几个相关性因素。为清晰说明起见，这里引入一个交通机动车模型。在模型中引入了有效载荷与用来抵消开支的收益［BRE 83］，据此可以简单地进行以下比较：

    ●在系统成本K_S中，重要的部分是开发的设计成本（K_D）与研发的轻量化附加成本（K_L）、材料成本（K_W）、工具成本（K_Wzg）与制造成本（K_F）：

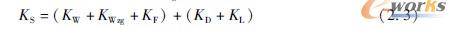
    轻量化附加成本（K_L）由工程师的工作量（ΔK_I）、试验（ΔK_V）与制造工具方面的额外开销（ΔK_Wzg）组成。
    ●这里，材料成本占成本的主要份额（约占系统成本K_S的35％～40%）由以下方程确定：

    其中，KWi为每个结构件的材料每千克的价格。
    ●运营成本与总重量成比例关系，可采用运营成本因子kB计算:
    KB≈kB·G（２.５）
    ●收入则与有效载荷成比例，可采用有效载荷因子kE计算：
    KE≈kE·GN（2.6）
    由于一个使用轻量化交通机动车的企业在收入和运营成本方面可施加的影响是有限的，因此所能努力做到的是在最大的意义下尽量限制轻量化附加成本。其目标是应当在尽可能低的系统成本下［WIE 84］实现结构的轻量化：
    ●一般来说，当通过更佳尺寸设计和结构简化降低结构重量时，轻量化附加成本将会更低。
    ●相反地，当通过精细化构造和采用更贵的材料降低结构重量时，轻量化附加成本将会提高。
    从经济观点考虑，一辆商用汽车的有效载荷应当明显高于其结构重量（GN≥GS），因为只有这样才可以尽快地抵消附加的开支。正如在机动车技术规格手册里一再强调的那样，通常来说，在机动车达到一定的重量关系时，其价值较高。但是，即使达到规划的整备重量（这也是以往所有假设的基础），也并不意味着研发成功，因此有必要根据下述方程表述的相互关系［HER 80］来采取相应的措施。

    也就是说，在设计上应该考虑到还有一个放大因子在起作用，即需要有针对结构甚至整套设备的附加措施，以确保在给定的行程内能运输同样大小的有效载荷。放大因子可如下确定：

    按照经验，放大因子一般在以下范围内变动：
    汽车制造：α≈1.1～15
    飞机制造：α≈2～3
    航天工业：α≥5
    如果出现超重的情况，可以考虑两种替代方案。
    ●替代方案一：有效载荷GN保持不变，结构（+ΔGＳ）必须重新设计。由此产生额外的开销，其比例关系大约为

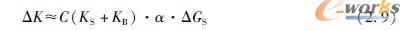
    ●替代方案二：降低有效载荷（－ΔGN），结构保持不变；则经济性变化比例关系大致为

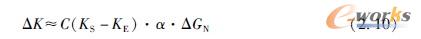
    具体应用中，需按照使用领域和约束条件来选择最合理的方案。