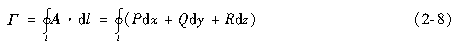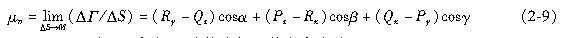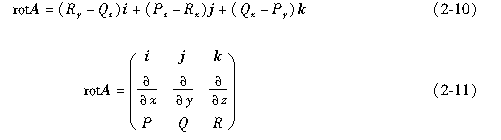2.1.1基础理论体系的组成
涡流制动型缓速器设计的计算与分析建立在大量数学理论和方法的基础上。这些理论和方法见于工程数学、电磁场理论、数值方法及机械设计等理论专著中,本书将其中适于缓速器设计的相关内容进行归纳统一,形成较为系统的基础理论体系框架。
涡流制动型缓速器设计涉及的基础理论和方法如图2-1a所示。在基础理论部分,矢量分析与场论、最优化方法、泛函与变分、矩阵理论等是最基本的数学基础,电磁场、温度场、流场和结构场等物理场的基本方程是其物理基础。基于力学理论的强度和刚度的设计方法、结构和电磁参数的优化设计方法、各类场量的数值模拟方法等是设计所用的基本方法。
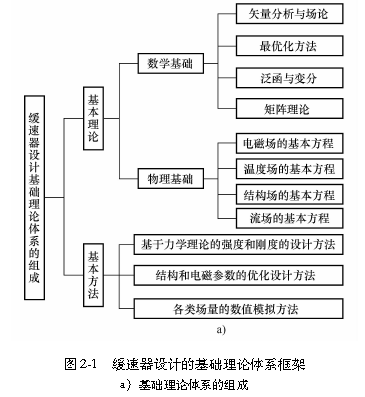
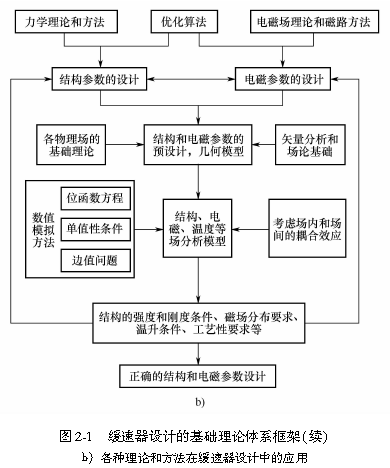
图2-1b所示为各种理论和方法在缓速器设计中的应用。在常规设计中,分别以力学理论和方法及电磁场理论和磁路方法为基础,结合优化方法,可预设计缓速器的结构参数和电磁参数,得到几何模型。应用各物理场理论和矢量分析与场论等数学方法,可建立预设计结果的结构场、电磁场、温度场、流场等场分析模型。采用适当的数值方法(如根据基本方程得到位函数方程,结合单值性条件,得到分析模型的边值问题)并考虑各物理场内部和场间的耦合效应,对该分析模型作数值模拟,得出各场量分布情况,确定结构的强度和刚度条件、磁场分布要求、温升条件、工艺性要求等是否满足。当满足这些条件和要求时,就会得到正确的结构和电磁参数设计结果,否则返回修改设计。
2.1.2缓速器中的物理场
如果在全部空间或部分空间里的每一点,都对应着某个物理量的一个确定值,则称在这个空间里确定了该物理量的一个场。根据该物理量是数量或矢量,分别称该场为数量场或矢量场,根据该物理量在该场中各点处的对应值是否随时间变化而变化,将该场区分为稳定场和非稳场(时变场)。
数量场用数性函数来表示:u=u(x,y,z)。用等值面表示数量u在场中的分布状况。由场中使函数u取相同数值的点所组成的曲面称为等值面,如温度场中的等温面、电位场中的等位面等。
与数量场一样,矢量场中分布的矢量A是场中之点M的函数A=A(M);在直角坐标系中,用其分量表示为A=A
x(x,y,z) i+A
y(x,y,z) j+A
z(x,y,z) k。每一点处,曲线都和对应于该点的矢量A相切的曲线称为矢量线,如静电场中的电力线、磁场中的磁力线、流场中的流线等,用矢量线可直观地表示矢量在场中的分布情况。
设有数性变量t和变矢A,如果对于t在某个范围G内的每一个数值,A都以一个确定的矢量与之对应,则称A为数性变量t的矢性函数,记为A=A(t),并称G为函数A的定义域。
在直角坐标系中,矢性函数A(t)的表达式为

矢性函数有与数性函数类似的导数(导矢)、微分和积分,在直角坐标系中可通过其数性分量求取其微分与积分,计算公式如下
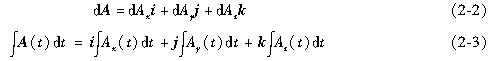
矢性函数广泛用于场的分析。
下面介绍数量场的方向导数和梯度。
1、方向导数
设M
0为数量场u=u(M)中的一点,从点M
0出发引一条射线l,在l上点M
0的邻近处取一动点M,记
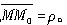
若当M→M
0时
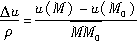
的极限存在,则称它为函数u(M)在点M
0处沿l方向的方向导数,记为
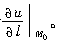
在直角坐标系中,若函数u=u(x,y,z) 在点M0(x
0,y
0,z
0)处可微,cosα、cosβ、cosγ为l方向的方向余弦,则函数u在点M
0处沿l方向的方向导数必存在,如下
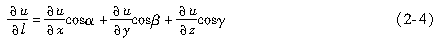
式中
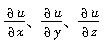
——点M
0处的偏导数。
2、梯度
若在数量场u(M)中的一点M处,存在这样一个矢量G,其方向为函数u(M)在点M处变化率最大的方向,其模也正好是此最大变化率的数值,则称矢量G为函数u(M)在点M处的梯度,记为gradu,即gradu=G。
在直角坐标系中,梯度的表达式为

如把数量场中每一点的梯度与场中点一一对应,则得一矢量场,称为该数量场产生的梯度场。
下面介绍矢量场的通量、散度、环量和旋度。
1、通量
沿矢量场A(M)中的有向曲面S某一侧的曲面积分
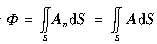
称为矢量场A(M)向积分所沿一侧穿过曲面S的通量。
在直角坐标系中,设A=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k,则通量可写为
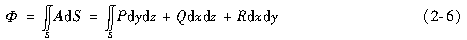
2、散度
设有矢量场A(M),于场中一点M的某个邻域内作一包含M在内的任一闭曲面ΔS,设其所包围的空间区域为ΔΩ,以ΔV表示其体积,以ΔΦ表示从其内穿出S的通量。若当ΔΩ沿任意方式缩向M点时,
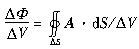
的极限存在,则称此极限为矢量场A(M)在点M处的散度,记为divA,是一数量。
散度由于是场中一点处通量对体积的变化率,所以又是该点处源的强度,其值为正、负或零时分别表示该点有正源(散发通量)、负源(吸收通量)或无源。
如把矢量场中每一点的散度与场中之点一一对应,则得一数量场,称为该矢量场产生的散度场。
在直角坐标系中,矢量场A=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k在任一点M(x,y,z)处的散度为

3、环量与环量面密度
设有矢量场A(M),则沿场中某一封闭的有向曲线l的曲线积分
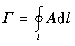
称为此矢量场按积分所取方向沿曲线l的环量。
在直角坐标系中,矢量场A=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k的环量为
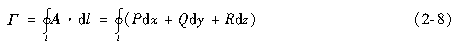
设M为矢量场A中的一点,在M点处取定一个方向n,再过M点任作一微小曲面ΔS,以n为其在M点处的法矢,对此曲面,又以ΔS表其面积,其周界Δl的正向取作与n构成右手螺旋关系,则矢量场沿Δl的正向的环量ΔΓ与面积ΔS之比,当曲面ΔS在保持M点与其上的条件下,沿着自身缩向M点时,若ΔΓ/ΔS的极限存在,则称其为矢量场A在点M处沿方向n的环量面密度,记为μ
n。
在直角坐标系中,环量面密度的计算公式为
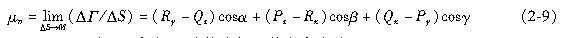
式中,cosα、cosβ、cosγ为ΔS在点M处的法矢n的方向余弦。
4、旋度
若在矢量场A中的一点M处存在这样的一个矢量R,矢量场A在点M处沿其方向的环量面密度为最大,该最大的数值正好就是R,则称矢量R为矢量场A在点M处的旋度,记为rotA,即rotA=R。显然,旋度在数值和方向上表示出了最大的环量面密度。
在直角坐标系中,旋度的计算公式为
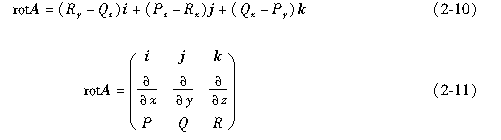
根据矢量场的Jacobi矩阵DA,可方便地求解矢量场的散度和旋度。
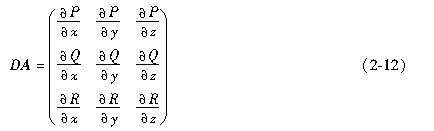
其对角线之和为散度,其余六个用于旋度公式中。
用矢量微分运算符Hamilton算子Δ表达的梯度、散度和旋度,如gradu=Δ u, divA=Δ·A,rotA=Δ×A。在以下的场量运算中将广泛地使用这些符号。
用Hamilton算子表达上述场量的一些重要性质,如Δ·(Δ×A)=0,Δ×(Δ×A)=Δ(Δ·A)-ΔA,Δ×(Δ u)=0,Δ·(A×B)=B·Δ×A-A·Δ×B等



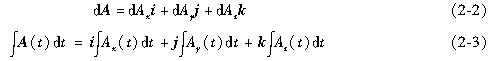
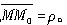 若当M→M0时
若当M→M0时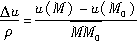 的极限存在,则称它为函数u(M)在点M0处沿l方向的方向导数,记为
的极限存在,则称它为函数u(M)在点M0处沿l方向的方向导数,记为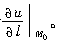
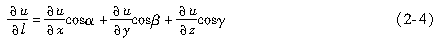
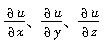 ——点M0处的偏导数。
——点M0处的偏导数。
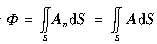 称为矢量场A(M)向积分所沿一侧穿过曲面S的通量。
称为矢量场A(M)向积分所沿一侧穿过曲面S的通量。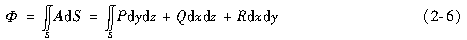
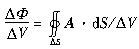 的极限存在,则称此极限为矢量场A(M)在点M处的散度,记为divA,是一数量。
的极限存在,则称此极限为矢量场A(M)在点M处的散度,记为divA,是一数量。
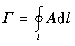 称为此矢量场按积分所取方向沿曲线l的环量。
称为此矢量场按积分所取方向沿曲线l的环量。