第二章 第2章 车辆简化模型及振动
第三节 2-3 双质量车身车轮振动
2.3.1双质量系统振动微分方程
对于双轴汽车四个自由度的振动模型,当悬挂质量分配系数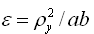 的数值接近1时,前后悬挂系统的垂直振动几乎是独立的,于是汽车可以简化为1/4汽车双质量2自由度系统振动模型,如图2-11所示。
的数值接近1时,前后悬挂系统的垂直振动几乎是独立的,于是汽车可以简化为1/4汽车双质量2自由度系统振动模型,如图2-11所示。
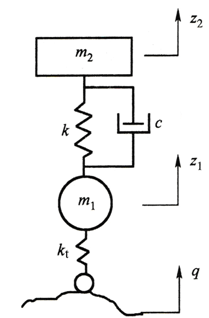
图2-11 单轮双质量2自由度模型
双质量系统振动模型,不仅可以反映的车身部分的动态特性,还能反映车轮部分在10~15Hz范围产生高频共振时的动态特性,它对平顺性和车轮的接地性有较大影响,比单质量系统更接近汽车悬挂系统的实际情况。设车轮与车身垂直位移坐标分别为Ζ1和Ζ2 ,坐标原点选在各自的平衡位置,则振动微分方程为
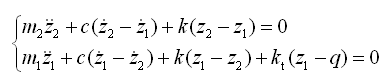 (2-50)
(2-50)
2.3.2双质量无阻尼系统的自由振动
当系统不计阻尼式,则双质量系统的自由振动微分方程变为
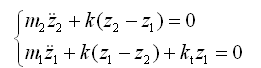 (2-51)
(2-51)
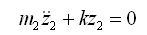
其固有圆频率为
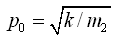
同样,若m2不动(z2 = 0),相当于车轮质量m1作单自由度无阻尼自由振动,于是可得
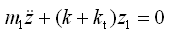 (2-52)
(2-52)
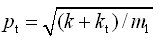 (2-53)
(2-53)
在无阻尼自由振动时,车身质量和车轮质量将以相同的圆频率ω和相角φ作简谐振动,设车轮和车身的振幅分别为z10和z20,则它们的振动响应分别为
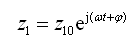 (2-54)
(2-54)
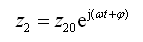 (2-55)
(2-55)
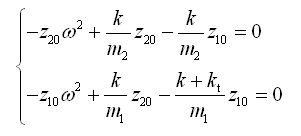 (2-56)
(2-56)
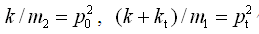 代入上式(2-56),可得
代入上式(2-56),可得
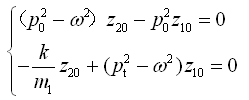 (2-57)
(2-57)
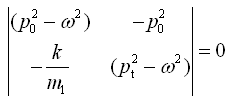
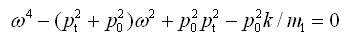 (2-58)
(2-58)
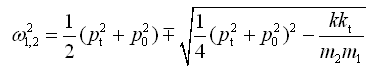 (2-59)
(2-59)
一阶主振型:
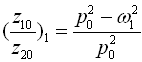 (2-60)
(2-60)二阶主振型:
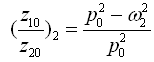 (2-61)
(2-61)例如,某汽车,车身固有圆频率Ρ0=2πrad/s,质量比rm=m2/m1=10,刚度比rk=kt/k=9,求系统的主频率和主振型。
由式(2-53)车轮的固有圆频率为
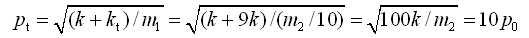
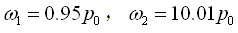
将两个主频率ω1和ω2分别代入式(2-60)和式(2-61),可确定两个主振型
一阶主振型:
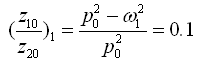
二阶主振型:
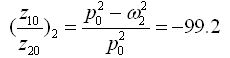
车身与车轮两个自由度系统的主振型,如图2-12所示。在强迫振动情况下,激振频率ω接近系统主频率ω1时将产生低频共振,按一阶主振型振动,车身质量m2的振幅比车轮质量m1的振幅大将近10倍。所以主要是车身质量m2在振动,称为车身型振动。
当激振频率ω接近系统主频率ω2时,产生高频共振,按二阶主振型振动,此时车轮质量m1的振幅比车身质量m2的振幅大将近100倍(实际由于阻尼存在而不会相差这样多),称为车轮型振动。
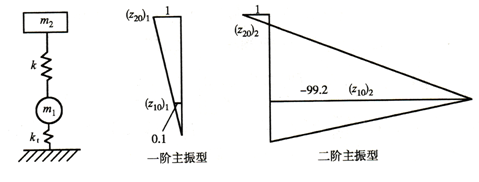
图2-12 两自由度系统的主振型
在图2-12中两自由度系统的车轮型振动,由于车身基本不动,所以可将两个自由度系统简化为图2-13所示车轮部分的单质量系统,来分析车轮部分在高频共振区的振动。
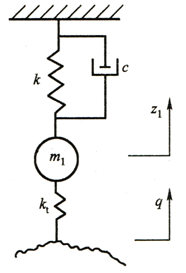
图2-13 车轮部分单质量系统
由图2-13可知,车轮质量m1的运动方程为
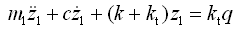 (2-62)
(2-62)
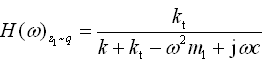
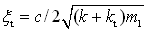 以及
以及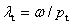 代入上式得
代入上式得
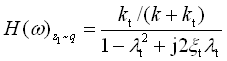
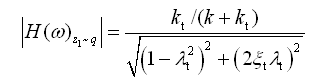 (2-63)
(2-63)
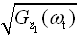 正比于车轮响应加速度
正比于车轮响应加速度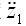 对路面激励速度
对路面激励速度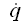 的幅频特性,即
的幅频特性,即
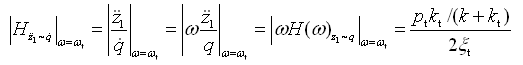 (2-64)
(2-64)
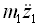 下降,车轮相对动载Fd/G降低,有利于提高车辆行驶安全性。
下降,车轮相对动载Fd/G降低,有利于提高车辆行驶安全性。2.3.3双质量振动系统的传递特性
先求双质量系统的频率响应函数,将有关各复振幅代入方程式(2-50),可得
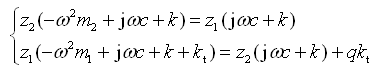 (2-65)
(2-65)
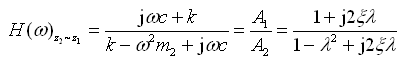 (2-66)
(2-66)
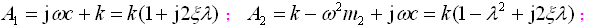 λ为频率比,λ=ω/p0;ξ为阻尼比,
λ为频率比,λ=ω/p0;ξ为阻尼比,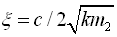 。
。由式(2-66)可知,双质量系统的车身响应z2对车轮响应z1的幅频特性|Η(ω)z2~z1|与单质量系统幅频特性|Η(ω)z~q|完全一样,即
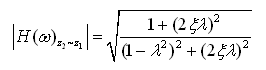 (2-67)
(2-67)
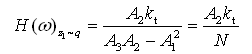 (2-68)
(2-68)
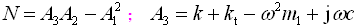 。
。由式(2-68)可得车轮响应z1对路面激励q的幅频特性|Η(ω)z1~q|,即
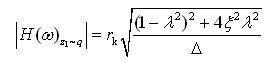 (2-69)
(2-69)
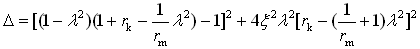 ;λ为频率比,λ=ω/p0;rk为刚度比,rk=kt/k;rm为质量比,rm=m2/m1。
;λ为频率比,λ=ω/p0;rk为刚度比,rk=kt/k;rm为质量比,rm=m2/m1。车身振动位移响应Z2对路面激励位移q的频率响应函数|Η(ω)z2~q|,由式(2-66)及式(2-68)两个环节的频率响应函数相乘,便可得到
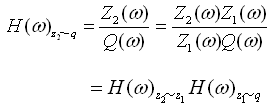
即 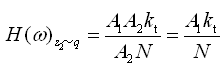 (2-70)
(2-70)
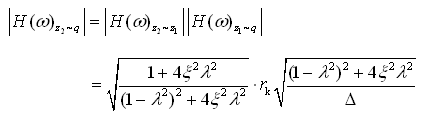
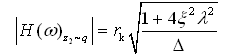 (2-71)
(2-71)图2-14、图2-15分别是对应式(2-69)和式(2-71)的幅频特性曲线。
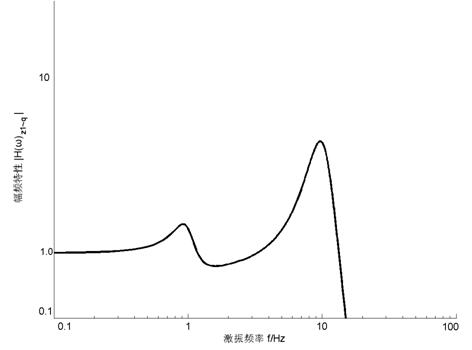
图2-14 Z1对q的幅频特性曲线图
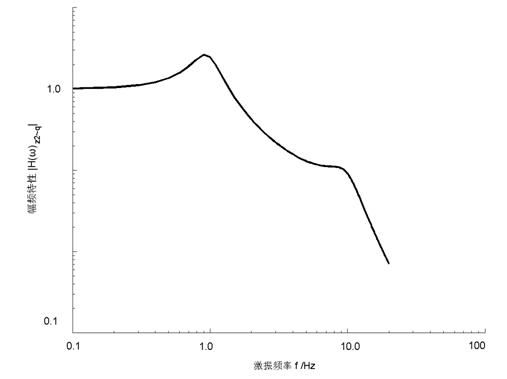
图2-15 Z2对q的幅频特性曲线
由图2-14和图2-15可以看出,对于这个车身车轮二自由度模型,当激振频率接近系统一阶固有频率ω1和二阶固有频率ω2时,都会发生共振,车身位移Z2对q幅频特性和车轮位移Z1对q的幅频特性,都有低频、高频两个共振峰。