第二章 第2章 车辆简化模型及振动
第四节 2-4 双轴汽车垂直和俯仰平面振动
前面讨论的单质量和双质量系统都是双轴汽车的局部系统,只分析了单输入下车身的垂直振动,实际汽车还存在整体的垂直振动和俯仰振动。现在进一步讨论汽车垂直和俯仰两个自由度振动系统,在前、后车轮的两个路面不平输入下的强迫振动。
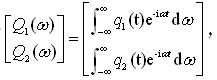 可得到响应的矩阵表达式为
可得到响应的矩阵表达式为
2.4.1双轴汽车垂直振动和俯仰振动微分方程
在分析车身振动时,忽略了车轮部分质量和轮胎刚度的影响,把汽车简化成图2-16(a)所示的二自由度系统。
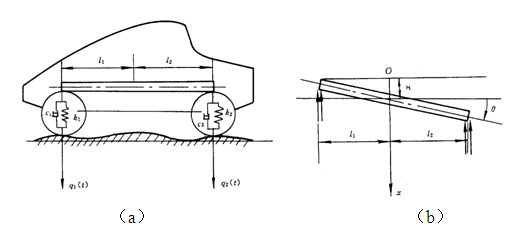
图2-16 双轴汽车振动模型
由于已知前、后悬挂的刚度κ1,κ2,阻尼c1,c2,车身质量m2,系统绕质心轴的转动惯量Jc=mρc2,质心到前后、悬挂的距离分别为ι1和ι2;设由于路面不平在前、后轮处产生的位移输入用q1(t)和q2(t)来表示;系统的坐标为质心偏离静平衡位置的铅垂距离x和绕质心的转角θ;x和θ的正向如图2-16(b)所示。根据图2-16(b)可写出车身的平面运动微分方程:
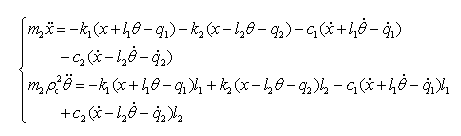
即 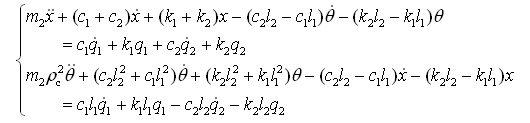 (2-72)
(2-72)
设χ2=ι1θ,χ1=χ代入上式,并引入下列参数:
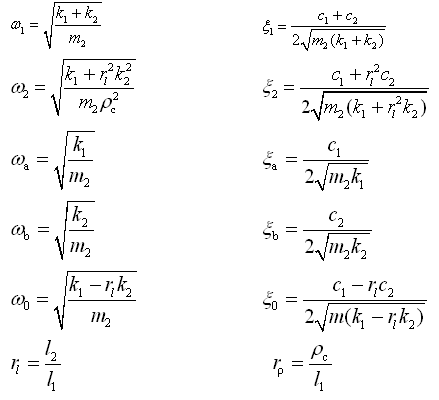
于是将式(2-71)简化为
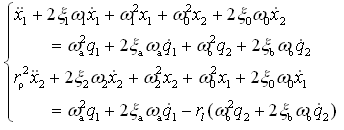 (2-73)
(2-73)
式中,ω为垂直振动的固有频率,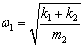 ;ω2为俯仰振动的固有频率,
;ω2为俯仰振动的固有频率,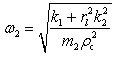
2.4.2双轴汽车振动频率响应函数及振动响应
求χ1,χ2对应于输入q1的频率响应函数Η11(ω),Η21(ω)。根据单位谐函数法,令
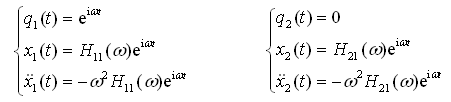
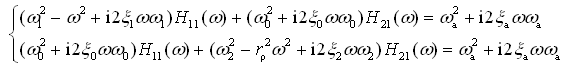
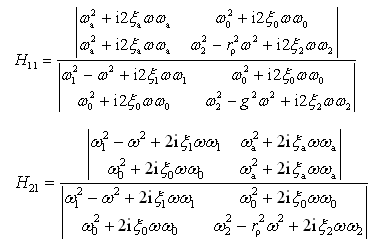
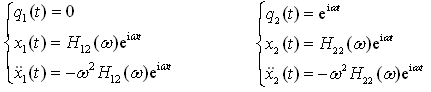
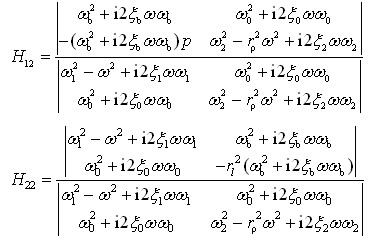
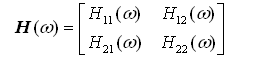 (2-74)
(2-74)
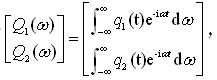 可得到响应的矩阵表达式为
可得到响应的矩阵表达式为
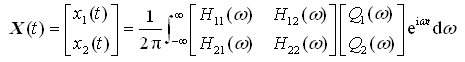 (2-75)
(2-75)