第二章 第2章 车辆简化模型及振动

2.5.1“人－车”系统振动模型

      在单轮模型基础上，增加乘员座椅模型，即为考虑乘员座椅的单轮模型，如图2-17所示。

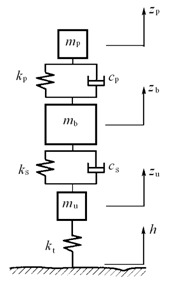
图2-17  考虑乘员座椅的单轮模型

 
      图2-17中，m_b为一个单轮上对应的车身质量，即簧上质量；k_s为车身悬架弹性系数；c_s为车身悬架阻尼系数；m_p为一个车轮上对应的座椅和人体质量；k_p和c_p分别是座椅弹性系数和阻尼系数；m_u为簧下质量，k_t为轮胎刚度。
      对于图2-17所示的三质量振动系统，其振动微分方程为

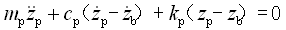      (2-76)    

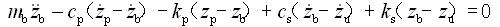     (2-77)

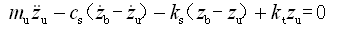         (2-78)

定义如下参数   
    ①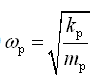，座椅-人体无阻尼固有频率；
    ②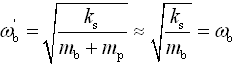，车身无阻尼固有频率；
    ③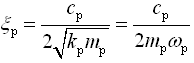，座椅-人体阻尼比；
    ④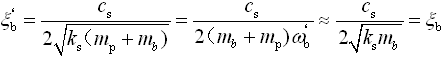，车身阻尼比；
    ⑤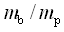，车身与人体的质量比；
    ⑥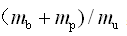，簧上与簧下的质量比；
    ⑦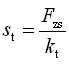，轮胎次切距，约等于轮胎静挠度；
    ⑧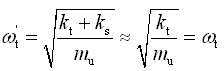，在无耦合、无阻尼的车轮固有频率；
    ⑨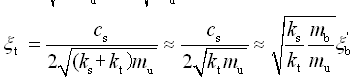（簧下质量阻尼比）
      根据式(2-76)～式(2-78），可以求出对行驶安全性有重要影响的车轮动载荷为

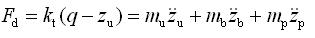         (2-79)

2.5.2振动响应传递特性

      为求出各响应量对路面不平度q的频率响应函数，对式(2-76)～式(2-78)两边求拉氏变换，其中，振动响应位移z_u，z_b和z_p的付氏变化分别为Z_u，Z_b和Z_p，路面不平度q的付氏变化为Q。因此，可求的振动位移响应z_u，z_b和z_p对路面不平度输入q的传递函数，它们分别为

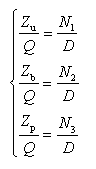                      (2-80)

式中，
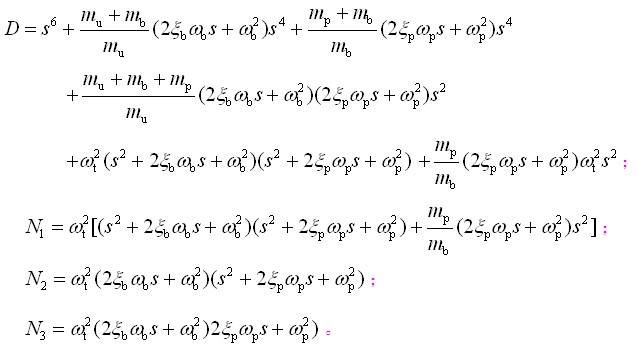      令z_u，z_b和z_p传递函数式（2-79）中的s=jω，即得到振动位移响应z_u，z_b和z_p对路面不平度输入q的频率响应函数，即

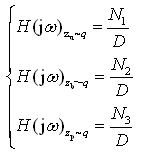                    (2-81)

      其它响应量和车轮动载荷F_d对路面激励位移q的频率响应函数，也可按照类似方法，求得以下关系求得

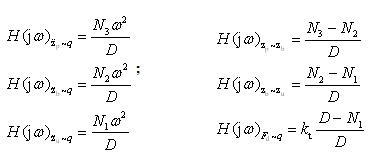                  (2-82)

      因此，根据各振动响应量对路面激励位移q的频率响应函数，便可以求得各振动响应量。